Here, you find my whole video series about Linear Algebra in the correct order and you also find my book that you can download for free. On this site, I also want to help you with some text around the videos. If you want to test your knowledge, please use the quizzes, and consult the PDF version of the video if needed. In the case you have any questions about the topic, you can contact me or use the community discussion in Mattermost and ask anything. Moreover, some older calculation videos are not included in the series but you can find them as additional videos. Now, without further ado, let’s start:
Part 1 - Introduction
Linear Algebra is a video series I started for everyone who is interested in calculating with vectors and understanding the abstract ideas of vector spaces and linear maps. The course is based on my book Linear Algebra in a Nutshell. We will start with the basics and slowly will climb to the peak of the mountains of Linear Algebra. Of course, this is not an easy task and it will be a hiking tour that we will do together. The only knowledge you need to bring with you is what you can learn in my Start Learning Mathematics series. However, this is what I explain in the first video. Moreover, you can also watch the overview video for the whole series where I explain the content of the series. If you are already an expert in basic Linear Algebra, you can also check out my Abstract Linear Algebra series where we immediately consider general vector spaces and related stuff.
Content of the video:
00:00 Introduction
00:50 Linear Algebra applications
02:20 Visit to the abstract level
03:00 Concrete level
03:40 Prerequisites
04:10 Credits
With this you now know already some important notions of linear algebra like vector spaces, linear maps, and matrices. Now, in the next video let us define the first vector space for this course. Some more explanation, you can find in my book:
Part 2 - Vectors in $ \mathbb{R}^2 $
Let us start by talking about vectors in the plane:

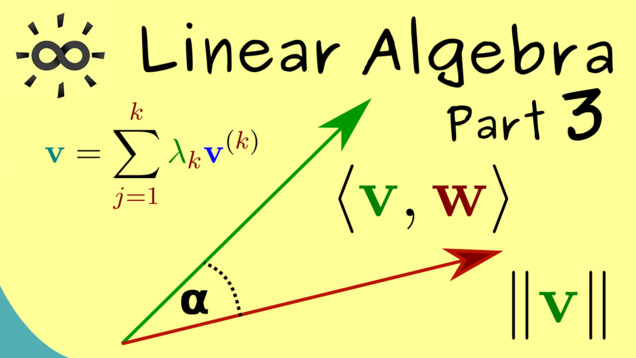
Part 3 - Linear Combinations and Inner Products in $ \mathbb{R}^2 $
Now we talk about linear combinations, the standard inner product and the norm:
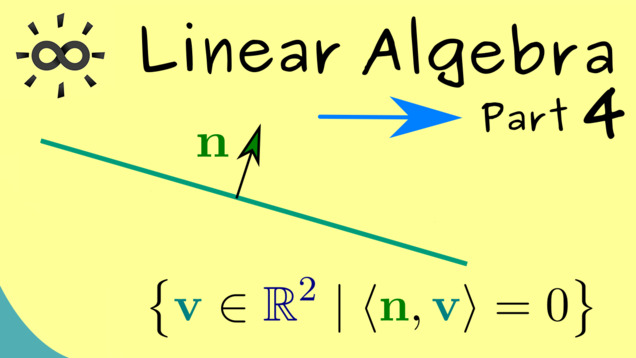
Part 4 - Lines in $ \mathbb{R}^2 $
With this, we are now able to define lines in the plane:
Part 5 - Vector Space $ \mathbb{R}^n $
Now we are ready to go more abstract. Let’s define a general vector space by listing all the properties such an object should satisfy. We can visualise this with the most important example.
Part 6 - Linear Subspaces
In the next video, we will discuss a very important concept: linear subspaces. Usually we just call them subspaces. They can be characterised with three properties.

Part 7 - Examples for Subspaces
I think that it will be very helpful to look closely at some examples for subspaces. Therefore, the next video will be about explicit calculations.

Part 8 - Linear Span
The next concept we discuss is about the so-called span. Other names one uses for this are linear hull or linear span. It simply describes the smallest subspace one can form with a given set of vectors.

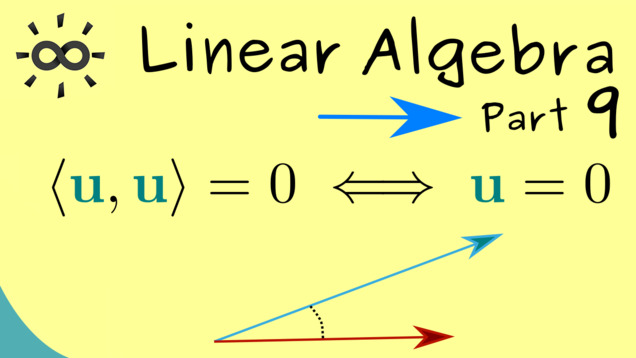
Part 9 - Inner Product and Norm
As for the vector space $ \mathbb{R}^2 $, we can define the standard inner product and the Euclidean norm in the vector space $ \mathbb{R}^n $.
Part 10 - Cross Product
In the next part, we will look at an important product that only exists in the vector space $ \mathbb{R}^3 $: the so-called cross product.

Part 11 - Matrices
When we want to solve systems of linear equations, it’s helpful to introduce so-called matrices:

Part 12 - Systems of Linear Equations
After introducing matrices, we can now see why they are so useful. They can be used to describe systems of linear equations in a compact form.

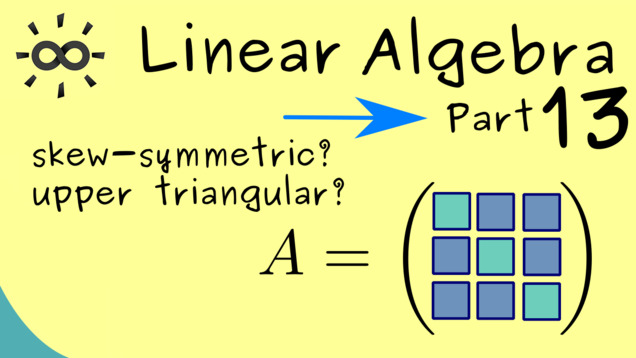
Part 13 - Special Matrices
In the next video, we go back to matrices. We will discuss some important names for matrices, like square matrices, upper triangular matrices, and symmetric matrices.
Part 14 - Column Picture of the Matrix-Vector Product
Let’s continue talking about the important matrix-vector multiplication we introduced while explaining systems of linear equations. In the next video, we discuss the so-called column picture of the matrix-vector product.

Part 15 - Row Picture
Similarly, we can look at the rows of the matrix, which leads us to the row picture of the matrix-vector multiplication.

Part 16 - Matrix Product
Now, we are ready to define the matrix product.

Part 17 - Properties of the Matrix Product
After defining the matrix product, we can go into the details and check which properties for this new operation hold and which don’t.
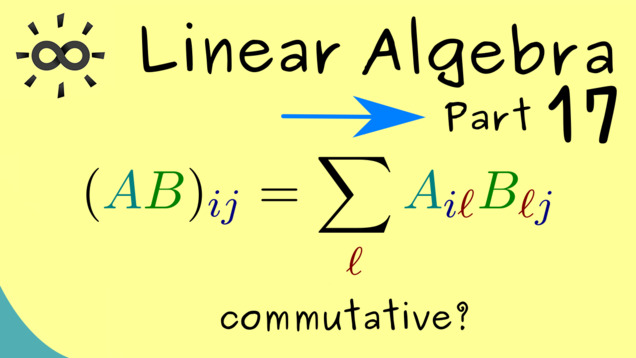
Part 18 - Linear Maps (Definition)
Let’s go more abstract again: we will consider so-called linear maps. They are defined in the sense that these maps conserve the linear structure of vector spaces.

Part 19 - Matrices induce linear maps
By knowing what a linear map is, we can look at some important examples. It turns out that all matrices induce linear maps.

Part 20 - Linear maps induce matrices
The converse of the statement of the previous video is also true. All linear maps induce matrices. This is an important fact because it means that an abstract linear map can be represented by a table of numbers.

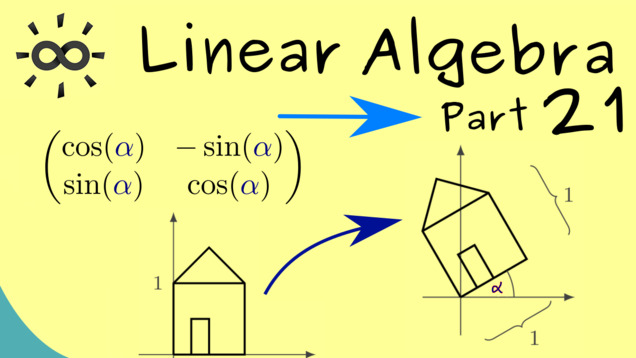
Part 21 - Examples of Linear Maps
Linear maps preserve the linear structure. This means that linear subspaces are sent to linear subspaces. Let’s consider some examples.
Part 22 - Linear Independence (Definition)
In the following video, we consider a new abstract notion: linear dependence and linear independence. We first explain the definition.

Part 23 - Linear Independence (Examples)
Now let’s consider examples of linearly independent families of vectors.

Part 24 - Basis of a subspace
Let’s discuss the concept of a basis.

Part 25 - Coordinates with respect to a Basis
Next, let’s talk how we calculate with bases. We define coordinates of vectors with respect to a chosen basis. Depending on the problem you want to solve, different bases might be helpful such that the coordinates you calculate with are simpler.

Part 26 - Steinitz Exchange Lemma
The next part will be more technical and about the so-called Steinitz Exchange Lemma. This will be used in some proofs later.

Part 27 - Dimension of a Subspace
After this technical proof, we are now able to define the concept of dimension. This is a natural number that describes the number of degrees of freedom in a subspace.

Part 28 - Conservation of Dimension
The dimension has a nice property that is conserved is some sense for linear maps.

Part 29 - Identity and Inverses
In the next videos, let us discuss some more concrete objects again. First, we look at matrices and define a special one: the identity matrix.

Part 30 - Injectivity, Surjectivity for Square Matrices
We recall the important notions for maps: injectivity and surjectivity. This concepts also hold for linear map and, therefore, can be transferred to matrices as well. Especially for square matrices, we find a very nice connection:
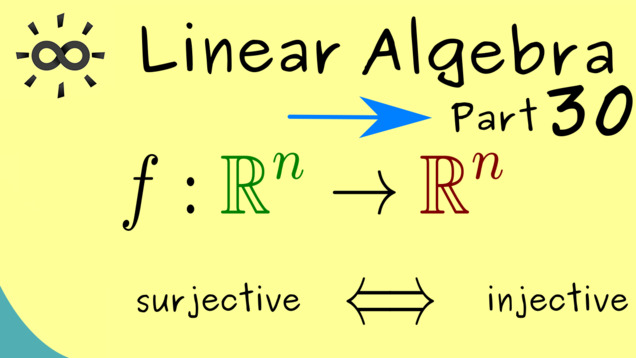
Part 31 - Inverses of Linear Maps are Linear
Let us quickly prove the important fact that, for bijective linear maps, the inverses are always also linear.
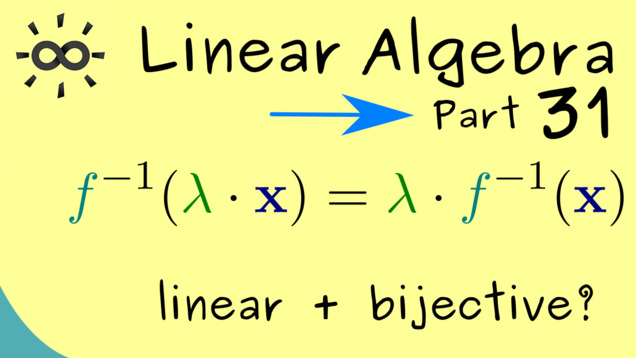
Part 32 - Transposition for Matrices
In the next video, we define a matrix operation: the transpose.
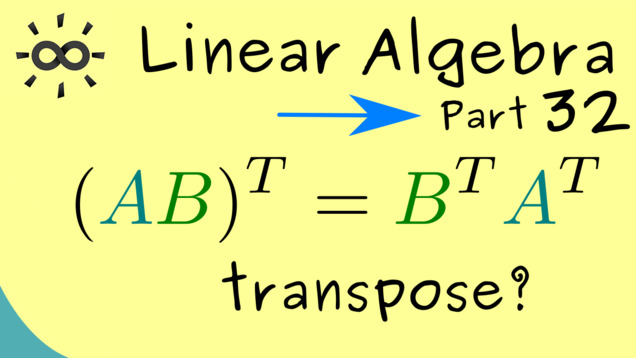
Part 33 - Transpose and Inner Product
The tranpose of a matrix could also be defined by using the standard inner product. This is an important relation that explains why the transpose is such a useful object.
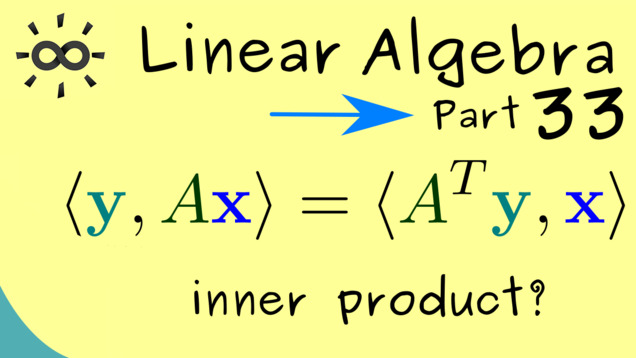
Part 34 - Range and Kernel of a Matrix
The following two definitions are very important for the rest of the course: the range of a matrix and the kernel of a matrix. Both are defined as sets in a vector space and it turns out that they are actually subspaces.

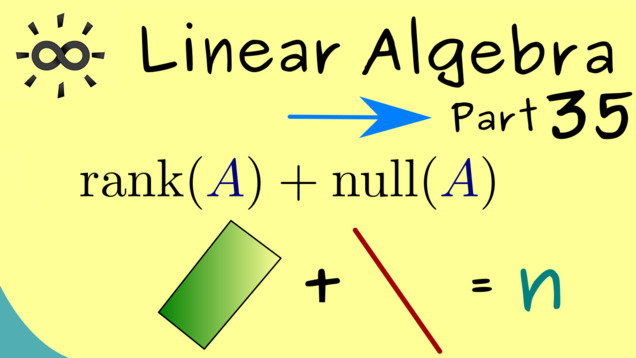
Part 35 - Rank-Nullity Theorem
Let’s immediately use the definitions from above in order to formulate a key property of linear maps and matrices: the rank-nullity theorem. In addition, we will also be able to prove this fact.
Part 36 - Solving Systems of Linear Equations (Introduction)
Now we go back to our motivation while doing linear algebra: we want to solve systems of linear equations. This video is like an introduction into this huge topic. After getting the rough idea how the solving process should work, we will go into more details with later videos.

Part 37 - Row Operations
What we need to solve systems of linear equations are so-called row operations. These can be described by using invertible matrices that are multiplied from the left-hand side.

Part 38 - Set of Solutions
Here, we will define the set of solutions for a system of linear equations. It’s denoted by $ \mathcal{S} $.

Part 39 - Gaussian Elimination
This is one of the most important topics in this course. It is not theoretically complicated but the applications are everywhere. The Gaussian elimination is always needed when you want to solve a system of linear equations in an algorithmic way.
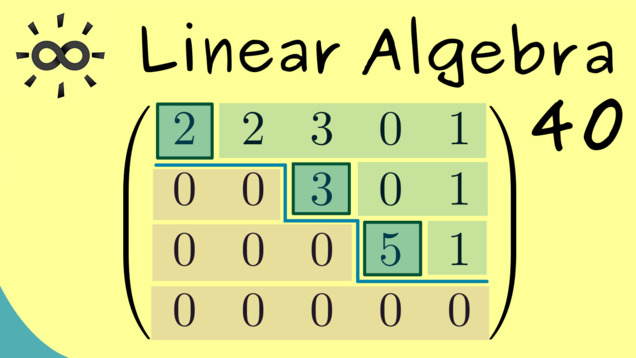
Part 40 - Row Echelon Form
Now, we are ready to define the important end result for the Gaussian elimination. This generalises a triangular form we have seen in former videos. It’s called row echelon form because the structure is given like a staircase.
Part 41 - Solvability of a System
Let’s discuss our result more abstractly now. We can always transform a system of linear equations into row echelon form. What does this say about the solvability of the system. It turn out that we can nicely formulate equivalent statements there.

Part 42 - Uniqueness of Solutions
The upcoming video will show in which cases we have a unique solution for a system of linear equations. This will be also the last video about the Gaussian elimination for now.

For a good application of the whole Gaussian elimination steps, see this video here
Part 43 - Determinant (Overview)
In the next videos, we will talk a lot about so-called determinants. First we will motivate them:

Content of the video:
00:00 Intro
00:50 Determinant of a matrix A
01:32 First property of determinant
03:40 Second property of determinant
04:57 Third property of determinant
06:50 Credits
Part 44 - Determinant in 2 Dimensions
In this video, we will see why a determinant makes sense for solving systems of linear equations and how we can calculate this determinant in two dimensions.

Part 45 - Determinant is a Volume Measure
Here, we introduce the notion of a volume measure in arbitrary dimensions. Please note that in 2 dimension, this coincides with the common area function we already discusses in the last video. Hence, we already now which rules a general volume function should fulfil. It turns out that these rules already determine the volume measure.

Part 46 - Leibniz Formula for Determinants
From the last video we can conclude a nice formula for the volume measure and, therefore, also for the determinant.
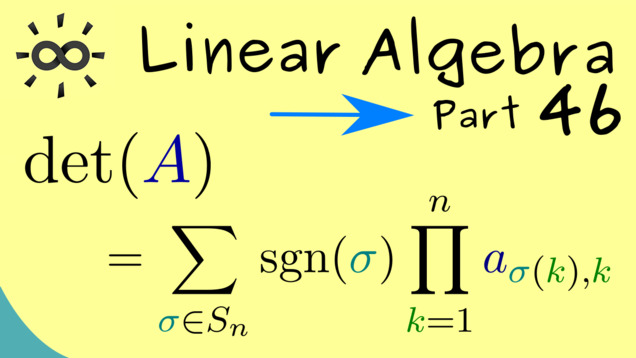
Part 47 - Rule of Sarrus
This is a mnenomic device to remember the Leibniz formula for a 3x3 determinant. It’s important to note that it only works there. For bigger matrices, one has too many terms such that a similar fast formula cannot exist.

Part 48 - Laplace Expansion
In this video, we will learn how to reduce a determinant recursively into smaller ones. For example, this is very helpful for a 4x4 determinant. There, we don’t have a compact formula. However, Laplace’s formula allows us to rewrite it, quickly, into four 3x3 determinants, for which we can use the rule of Sarrus.

Part 49 - Formulas for Determinants
This video covers very important properties of the determinant. In particular, we will discuss that the determinant is a multiplicative function. This means we can split the determinant for a product of matrices into the product of two determinants.

Content of the video:
00:00 Intro
00:44 Determinant for triangular matrices
02:17 Determinant for block matrices
06:00 Determinant for the transpose
06:50 Multiplication Rule for the determinant
09:41 Credits
Part 50 - Gaussian Elimination for Determinants
In this last video about calculation methods for the determinants, we build a bridge to the Gaussian elimination. We know that row operations can be described as matrix multiplications from the left. Hence, by using the multiplication rule of the determinant, we know how the determinants changes when applying row operations.
Part 51 - Determinant for Linear Maps
Before we have talked a lot about how to calculate determinants of matrices but we didn’t talk about an abstract generalisation. In fact, it’s straightforward to define the determinant for linear maps as well.
Part 52 - Cramer’s Rule
This is the last video covering the topic of determinants. First we state the important fact that invertibility of a matrix is equivalent to a non-vanishing determinant. After that we discuss the so-called Cramer’s rule. This one has a nice theoretical description for the unique solution of a system of linear equations that uses determinants. However, in general, this rule is not very efficient for actual calculations.
Content of the video:
00:00 Intro
01:05 Determinant in two Dimensions
02:10 Determinant and singular matrices
02:30 Proposition for non-singular matrices
04:41 Cramer’s Rule
07:30 Proof of Cramer’s Rule
12:27 Credits
Part 53 - Eigenvalues and Eigenvectors
After the long discussions of determinants, we start another very important topic of linear algebra: eigenvalues of square matrices. We start by discussing the definitions and looking at examples for 2x2 matrices.

Part 54 - Characteristic Polynomial
Now, in this video, we want to show how we can actually determine all eigenvalues of a given matrix. The key element will be the so-called characteristic polynomial. Before we start with the definition, we also discuss that eigenvectors can form a optiomal coordinate system if enough of them exist.

Part 55 - Algebraic Multiplicity
Let’s go deeper into the theory of eigenvalues and eigenvectors. For this we need a classical result from Gauß (1799): the fundamental theorem of algebra. It’s states that every polynomial over the complex numbers can be rewritten as a product of linear factors.

Part 56 - Geometric Multiplicity
After introducing the algebraic multiplicity, coming from the characteristic polynomial, we will now define the so-called geometric multiplicity. The name already gives the hint that this one explains how many different directions the eigenvectors can have.

Part 57 - Spectrum of Triangular Matrices
Triangular matrices are known from the Gaussian elimination and play an important role. It turns out that the eigenvalues can directly be calculated, even if the matrix is only in a block triangular structure. In this video, we will explictly look at some examples.

Part 58 - Complex Vectors and Complex Matrices
Since eigenvalues are given by the zeros of the characteristic polynomial, one inevitably stumbles across complex numbers. Indeed, the whole eigenvalue theory gets better if one includes complex matrices and complex vectors. Therefore, we will extend all the definitions from Linear Algebra to the complex realm.

Part 59 - Adjoint
Now, let’s define the so-called adjoint of a complex matrix. It is the equivalent of the transpose from the real case.

Part 60 - Selfadjoint and Unitary Matrices
The following video shows one of the most important results in the eigenvalue theory, namely that so-called selfadjoint matrices have only real numbers as eigenvalues. Moreover, we will also show that so-called unitary matrices have spectrum on the unit circle.

Part 61 - Similar Matrices
The notion of similar matrices is used to capture essential features of linear transformations. One often says that similar matrices represent the same linear map in different coordinate systems. Here, we will show that similar matrices have the same eigenvalues.
Part 62 - Recipe for Calculating Eigenvectors
The following video collects our knowledge from everything we learnt so far about eigenvectors. Therefore, this is not a theoretic video but a very practical one since we present an explicit example calculation.

Part 63 - Spectral Mapping Theorem
Here, we discuss the so-called spectral mapping theorem, which explains what happens to eigenvalues under maps. More precisely, we will put a matrix into a polynomial function and ask what the spectrum of this new matrix is.
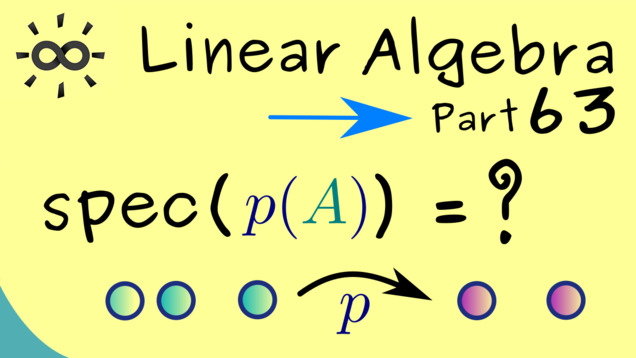
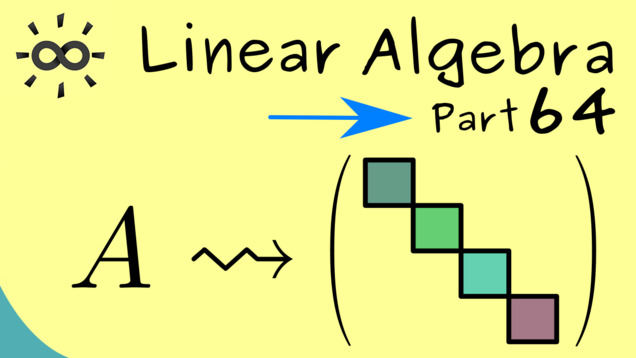
Part 64 - Diagonalization
This is one the most important matrix decompositions. We want to write a square matrix $ A $ in the form $ X D X^{-1} $ where $ D $ is a diagonal matrix. Obviously, one can easily calculate with such a diagonal matrix and therefore this decomposition is very helpful in applications. The whole process is called diagonalization.
Part 65 - Diagonalizable Matrices
We end this series with another discussion about diagonalization. Namely, we define so-called diagonalizable matrices, which can be transfered into a diagonal matrices. It turns out that we just need to compare algebraic and geomtetric multiplicities of eigenvalues to decided if a matrix is a diagonalizable one.
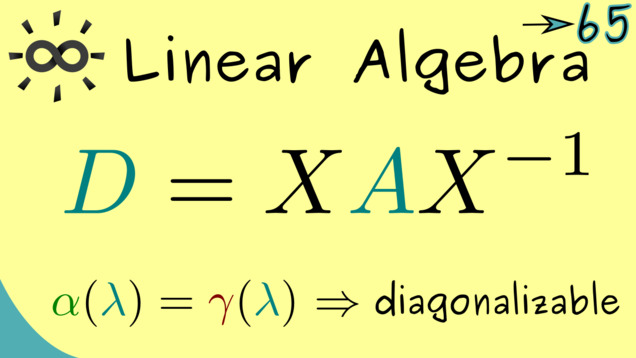
This was the last video in the series but not the last video about the topic of Linear Algebra. We continue developing the whole theory in the next series, which we call Abstract Linear Algebra. There we will finally define general vector spaces and calculate in an abstract way. If you want some concrete calculations, you can also check out some additional videos. For example, you get explanations about the Jordan Normal Form, the so-called QR decomposition, the simplified LU decomposition, and the important general PLU decomposition.
Connections to other courses
Summary of the course Linear Algebra
- You can download the whole PDF here and the whole dark PDF.
- You can download the whole printable PDF here.
- Test your knowledge in a full quiz.