Here, you find my whole video series about Hilbert spaces in the correct order and I also help you with some text around the videos. If you want to test your knowledge, please use the quizzes, and consult the PDF version of the video if needed. When you have any questions, you can use the comments below and ask anything. However, without further ado let’s start:
Part 1 - Introductions and Cauchy-Schwarz Inequality
Let’s start with a short overview for the whole course and with the important definition of an inner product. This is something we have alreade discussed in Linear Algebra but now we also add an particular analysis part to it: we want to have completeness of the underlying normed space. In short, we have the following: a Hilbert space is an inner product space and a Banach space in one. We also use the first video here to prove the famous Cauchy–Bunyakovsky–Schwarz inequality.
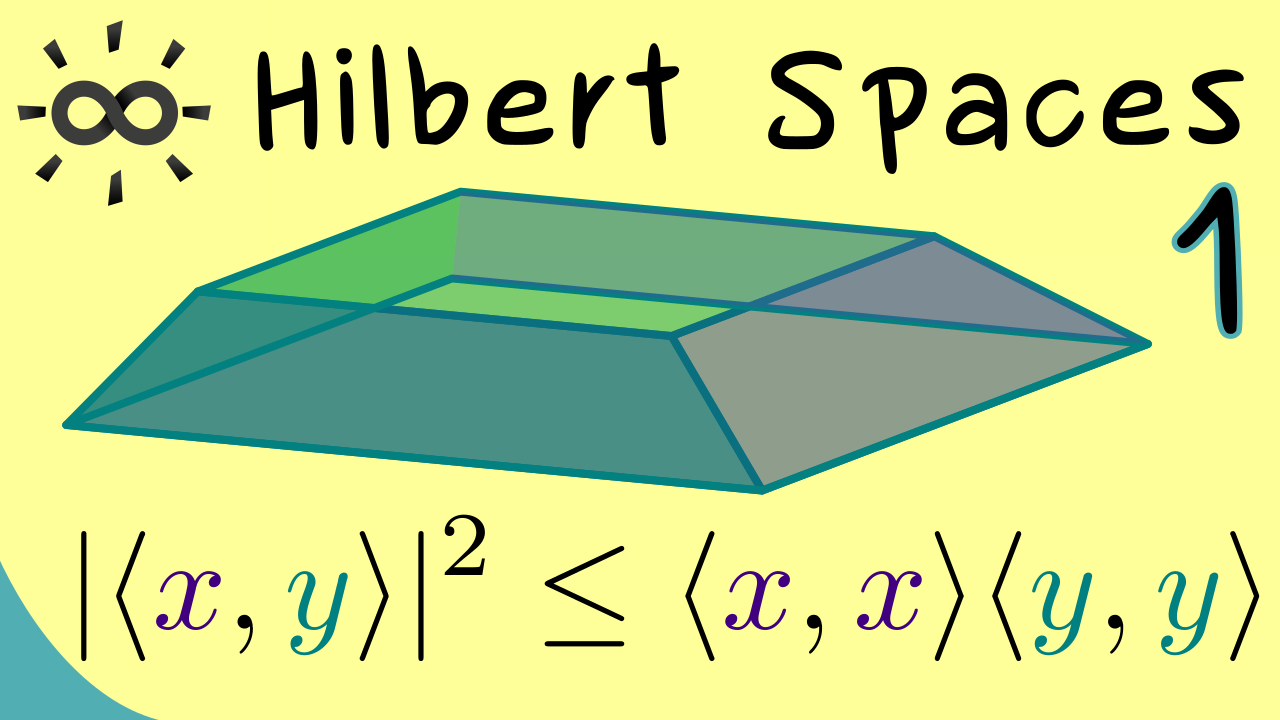
Content of the video:
00:00 Introduction
00:45 Network for the video courses
01:40 Prerequisite for the course
02:27 Topics in Hilbert Spaces
03:53 Definition for inner product spaces
06:53 Pre-Hilbert space as an alternative name
07:11 Cauchy-Schwarz inequality
07:53 Proof of Cauchy-Schwarz
11:20 Norm on inner product spaces
11:57 Definition of Hilbert space
12:34 Credits
Part 2 - Examples of Hilbert Spaces
Now we are ready to look at some examples for inner product spaces which are also complete. From the Functional Analysis series, we already know the important $ \ell^2 $-space. It consists of sequences which are also square-summable. It turns out that one can generalize this example to a so-called $ L^2(\Omega, \mu) $-space. It consists of functions defined on a measure space $(\Omega, \mathcal{A}, \mu) $.
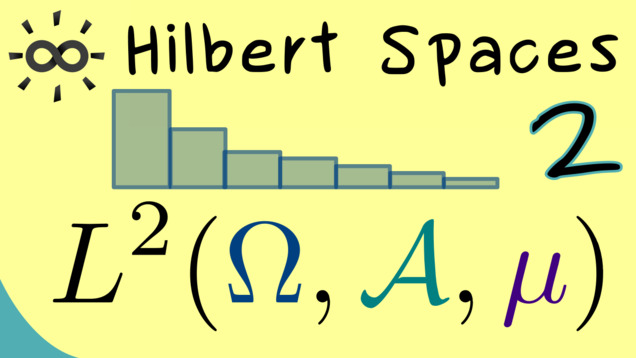
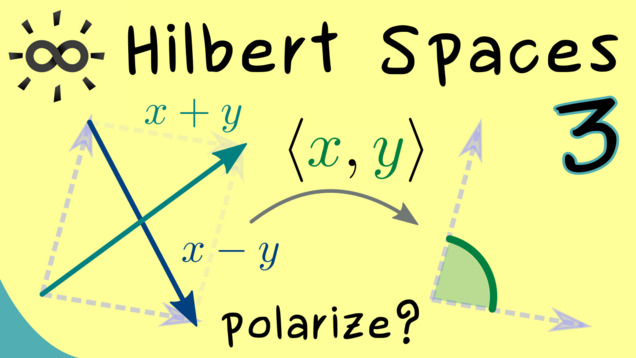
Part 3 - Polarization Identity
The polarization vividly describes what one can do with an inner product. Namely, one can decompose it into basic parts. And it turns out that the knowledge of the associated norm is enough to describe these basic parts.
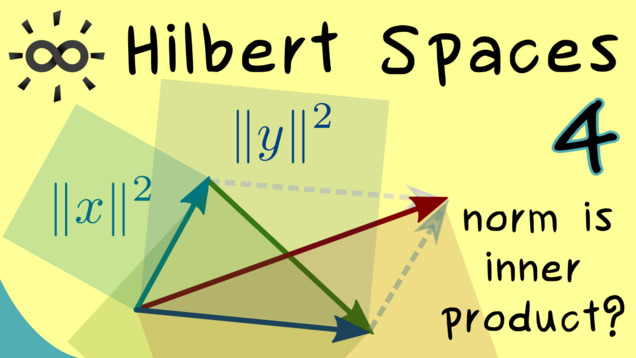
Part 4 - Parallelogram Law
In the next video, we will discuss the parallelogram law which holds in every inner product space. However, the formulation of this formula only uses the induced norm, so the question arises if the rule can also hold in general normed spaces. It turns out that the parallelogram law actually characterizes normed spaces which are also inner product spaces.
Part 5 - Proof of Jordan-von Neumann Theorem
The statement from the last video is also known as the Jordan-von-Neumann theorem. Let’s discuss the ideas of the proof of that.
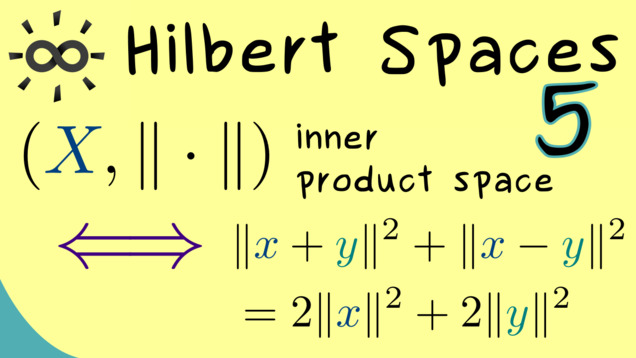
Part 6 - Orthogonal Complement
The whole advantage of Hilbert spaces, and also inner product spaces in general, is that we have a geometry we can calculate with. One part of the geometry we already received: we can measure lengths with the induced norm $ | \cdot | $. However, an inner product has much more than that. We can also measure angles with it. More precisely, we can easily define what we mean by a right angle, which means that we can say when two vectors are perpendicular. This is the concept of orthogonality which every inner product space carries. Moreover, we can also define the so-called orthogonal complement for each subset in the space.

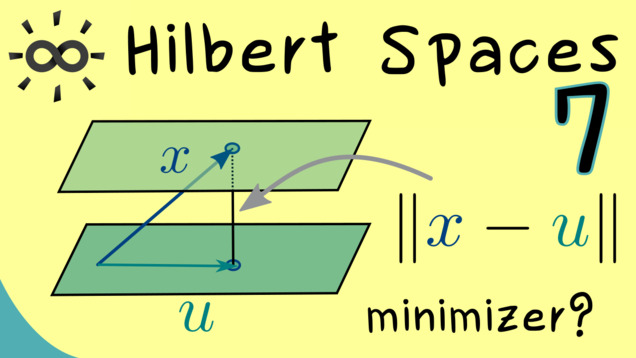
Part 7 - Approximation Formula
By using the orthogonality in inner product spaces, we can construct abstract right-angled triangles. It turns out that we also have the Pythagorean theorem in a general version there. Moreover, we should also be able to find orthogonal projections like we did in Linear Algebra. The key step for these is given by the approximation formula.
Part 8 - Proof of the Approximation Formula

Summary of the course Hilbert Spaces
- You can download the whole PDF here and the whole dark PDF.
- You can download the whole printable PDF here.
- Ask your questions in the community forum about Hilbert Spaces
Ad-free version available:
Click to watch the series on Vimeo.