Here, you find my whole video series about Complex Analysis in the correct order and I also help you with some text around the videos. If you want to test your knowledge, please use the quizzes, and consult the PDF version of the video if needed. When you have any questions, you can contact me or use the community discussion in Mattermost. You can also download a book about this course here, but it is still in the draft version. So without further ado let’s start:
Part 1 - Introduction
Complex analysis is a video series I started for everyone who is interested in calculus with the complex numbers and wants to expand her knowledge beyond the calculus with real numbers. Some basic facts from my Real Analysis course is needed but always mentioned in the videos.

Content of the video:
00:00 Introduction
02:13 What we need
03:18 Metric space
04:43 Sequences and convergence in ℂ
07:32 Continuity for complex functions
09:30 Endcard
With this you now know the foundations that we will need to start with this series. Some important bullet points are sequences, continuity, and derivatives for real functions. Then we will always expand the notions to the complex realm. Now, in the next video let us discuss what a derivative for a complex function is.
Part 2 - Complex Differentiability
The notion of a derivative is fundamental in a lot of mathematical topics. In my real analysis course, you already learnt how to define it. It is literally the same for the complex functions. However, the conclusions from this definition we can form might be different. In the next video, we can immediately define what it means that a function is complex differentiable. Since this is a local property, we have to fix a point in the domain of the function. However, in order to be meaningful, the domain should be an open set. This is a general concept, we will also explain now:

Content of the video:
00:00 Intro
01:21 Definition of open set in ℂ
03:22 Definition of differentiability in ℂ
07:01 Endcard
Part 3 - Complex Derivative and Examples
Now we define the complex derivative for a function and explain the linear approximation we get from this. We also explain some examples:

Content of the video:
00:00 Intro
00:34 The [geometric] intuition for complex derivative
04:11 Producing the formal definition
05:19 Example 1: A linear polynomial in ℂ
07:34 Example 2: A conjugate function
Part 4 - Holomorphic and Entire Functions
Now we explain the terms holomorphic function and entire function:
Content of the video:
00:00 Intro
00:28 How to define a holomorphic function?
02:29 Essential properties of holomorphic functions
04:21 Example 1. A complex polynomial
06:11 Example 2. A ‘rational function’ for polynomials
Part 5 - Totally Differentiability in $ \mathbb{R}^2 $
Let us translate a complex function to a real function:

Content of the video:
00:00 Intro
00:19 Is differentiation in ℂ and ℝ² the same?
01:43 Each complex function induces a real function
06:01 When is a map totally differentiable?
10:11 The meaning of Jacobian matrix and example
Part 6 - Cauchy-Riemann Equations
And now we are finally able to talk about the important Cauchy-Riemann equations:

Content of the video:
00:00 Intro
00:16 Two notions of differentiability
06:39 When is the vector-matrix multiplication a complex multiplication?
09:04 Deriving the Cauchy-Riemann equations
Part 7 - Cauchy-Riemann Equations Examples
Let’s now look at examples for the Cauchy-Riemann equations:

Content of the video:
00:00 Intro
00:18 Quick recap
02:42 Example 1: Identity function
04:28 Example 2: Complex conjugate function
05:38 Example 3: Complex polynomial
Part 8 - Wirtinger Derivatives
The following Wirtinger derivatives can be very helpful in quick calculations and give a nice short formula for the Cauchy-Riemann equations:
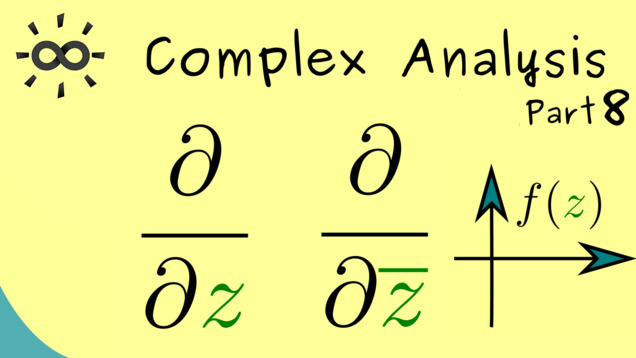
Content of the video:
00:00 Intro
00:19 Wirtinger derivatives — basic definition
01:35 Complex derivative through Cauchy-Riemann equations
05:12 Wirtinger derivatives — detailed definition
06:17 Example for z²
08:39 Summary: a criteria for holomorphic functions
Part 9 - Power Series
Now let us talk about power series:

Content of the video:
00:00 Intro
00:57 Why are power series important? Example of exp(z)
02:05 General definition
04:03 Example. Geometric series + conditions for convergence
09:06 Cauchy-Hadamard theorem
Part 10 - Uniform Convergence
When we talk about power series, the notion of uniform convergence is very important:

Content of the video:
0:00 Intro
0:40 Uniform convergence definition
2:17 Power series are holomorphic
2:31 Correction: codomain for the power series should be given by ℂ
3:25 Uniform convergence for power series
7:01 Credits
Part 11 - Power Series Are Holomorphic - Proof
Let us prove this important fact about power series:
Content of the video:
00:00 Intro
00:21 Recap: results for power series
1:52 Proof of the first result (convergence of a k-power series)
6:50 Proof of the second result (convergence of a k-1-power series)
8:46 Proof of the third result (complex differentiability)
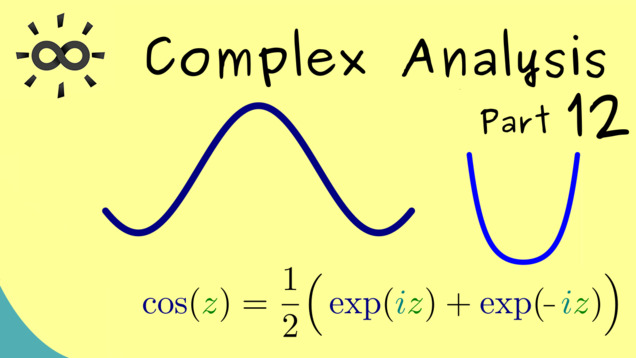
Part 12 - Exp, Cos and Sin as Power Series
Now let’s talk about the important functions Exp, Cos, and Sin as power series:
Content of the video:
00:00 Intro
00:12 Derivatives of power series
01:28 Exponential function as a power series
03:28 Cosine as a power series
08:56 Sine as a power series
Part 13 - Complex Logarithm
By knowing the exponential function, we can also define the inverse function, the logarithm. However, in the complex numbers, this is more complicated than in the real numbers.

Content of the video:
00:00 Intro
00:12 Logarithm as inverse of exponential function
00:33 How it works in the real numbers
01:54 Complex exponential function
03:08 exp(iy) lies on the unit circle
04:00 Definition of π
06:05 Exponential is 2πi-periodic
06:49 Exp is not injective
08:40 Restrict to open strip and slotted plane
09:06 Definition of logarithm (principal value)
09:56 Properties of logarithm
12:22 Credits
Part 14 - Powers
After the definition of the logarithm, we are able to define the power in the complex numbers:
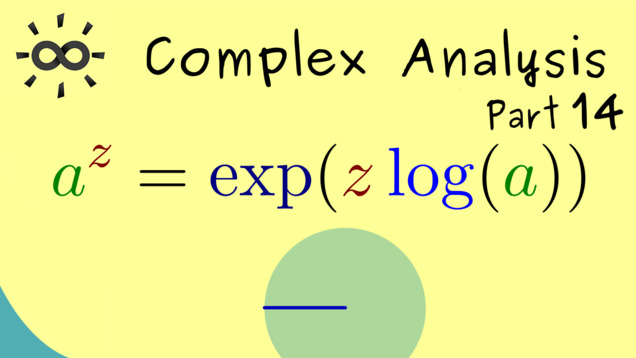
Content of the video:
00:00 Intro
00:14 Powers with complex numbers
01:06 Power definition in the real numbers
03:45 Using logarithm to write powers
04:50 Power definition in the complex numbers
06:05 What to do with a complex base?
07:00 Principal value of the power function
08:48 Credits
Part 15 - Laurent Series
Let’s start with a very important concept: Laurent series. One could say that they generalise power series.

Content of the video:
00:00 Intro
00:14 Generalization of power series
00:47 Radius of convergence
01:35 Consider inverse of complex numbers
02:20 Second radius of convergence for outside world
02:56 Series with negative powers is holomorphic
04:15 Two series combined gives holomorphic function
05:43 Definition Laurent Series
06:42 Principal part of Laurent Series
06:55 Residue of Laurent Series
07:20 Domain is a generalized ring
08:06 Credits
Part 16 - Isolated Singularities
After knowing what Laurent series are, we are able to talk about another important concept: isolated singularities. These are also important for holomomorphic functions that are not defined on the whole complex plane.

Part 17 - Complex Integration on Real Intervals
Now we are finally ready to extend the integral into the complex realm. We start with defining the integral for functions on real intervals:

Part 18 - Complex Contour Integral
In the next step, we can talk about the important contour integral in the complex plane. We start with the definition and look at some simple examples.

Part 19 - Properties of the Complex Contour Integral
Now we extend the complex integral to piecewise continuously differentiable paths and talk about important properties of the contour integral.

Part 20 - Antiderivatives
In the next video, we introduce primitives for complex-valued functions. A more suitable name is just antiderivatives. They can be used to calculate contour integrals.

Part 21 - Closed curves and antiderivatives
Building on the former video, we can also look at the converse statement. Can we conclude from the fact that contour integrals along closed curves are zero that an antiderivative has to exist?
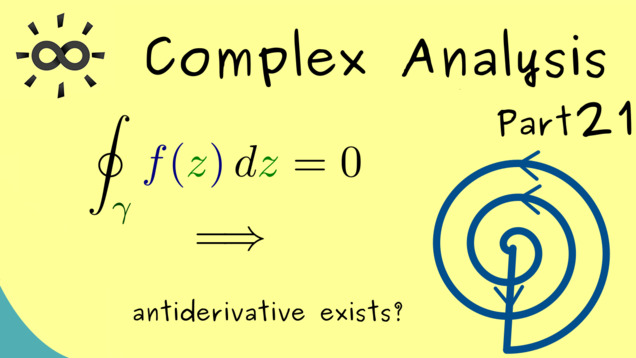
Part 22 - Goursat’s Theorem
Now, we are ready to formulate and prove the famous integral theorem known as Goursat’s Theorem.

Part 23 - Cauchy’s theorem
So let’s generalise the last result and formulate Cauchy’s theorem for discs.

Part 24 - Winding Number
In the next video, let’s go back to curves in the complex plane. We have learnt with Cauchy’s theorem that it is important to know if a curve lies in a disc for the domain of definition of a function. This guarantees that no point outside of the domain gets surrounded by the curve. This is essential for applying Cauchy’s theorem like the counterexample of the function $ f(z) = \frac{1}{z} $ shows us. Therefore, in order to generalise the theorem, we need to talk about winding number for curves and points.

Part 25 - Cauchy’s Theorem (general version)
After learning how Cauchy’s integration theorem works for discs, we can generalise it to other domains than just the disc. In particular, we can explicitly prove Cauchy’s Theorem for more domains. The most important one is one that looks like a keyhole and it will play an important role later. In the PDF version of this video, you find some detail explanation how to adjust the proof of part 23 in this case. Moreover, without an explicit proof, we also state the general version of Cauchy’s Theorem which does not need a requirement for the domain anymore.

Part 26 - Keyhole contour
In the following video, we will talk about a very special contour integral. We call it a keyhole contour because it looks like it. By using Cauchy’s integral theorem, we can show a very important fact for holomorphic functions with an isolated singularity.

Part 27 - Cauchy’s Integral Formula
And now finally, we can prove one of the most important formulas in Complex Analysis: Cauchy’s Integral Formula

Part 28 - Holomorphic Functions are C-infinity Functions
In the next part, we will generalise Cauchy’s integral formula also for derivatives. While doing this, we also show that each holomorphic can locally be represented by power series. In particular, this shows that each holomorphic function is a $ C^\infty $-function.

Part 29 - Liouville’s Theorem
The following result is very famous. It’s Liouville’s Theorem. It states that each entire is either constant or unbounded. In order to prove this fact, we will need Cauchy’s inequalities, which explain how much the derivatives of holomorphic functions can grow.

Part 30 - Identity Theorem
As a consequence from the last results, we can prove the famous identity theorem.

Part 31 - Application of the Identity Theorem
Next, let’s see some nice applications of the identity theorem from above.

Part 32 - Residue
The residue is an important notion in Complex Analysis.

Part 33 - Residue for Poles
Of course, the residue is only helpful as a concept if we can find additional calculation rules for it. For isolated singularities that are so-called poles we find a very nice formula:
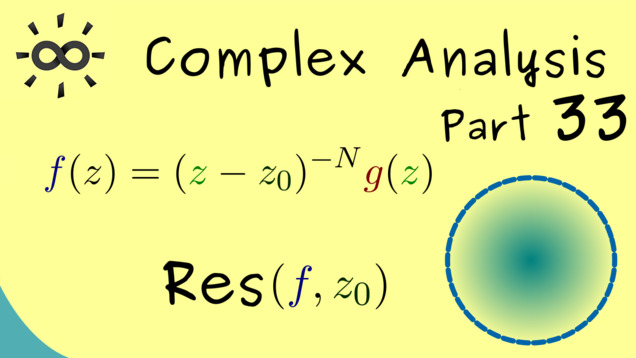
Part 34 - Residue theorem
Now, we have finally reached to point to formulate the popular residue theorem. We also give a short sketch of the proof.

Part 35 - Application of the Residue Theorem
To end this series for the moment, we show how we can use the residue theorem to calculate a real integral with it.

Summary of the course Complex Analysis
- You can download the whole PDF here and the whole dark PDF.
- You can download the whole printable PDF here.
- Test your knowledge in a full quiz.
- Ask your questions in the community forum about Complex Analysis
Ad-free version available:
Click to watch the series on Vimeo.