Here, you find my whole video series about Distributions in the correct order and I also help you with some text around the videos. If you have any questions, you can use the comments below and ask anything. However, without further ado let’s start:
Part 1 - Motivation and Delta Function
Distributions is a video series I started for everyone who is interested in calculating with generalised functions in the realm of partial differential equations or in physics. We will start with an overview and quickly define the new concepts in a rigorous way. It will be helpful if you have some knowledge in the basics of Linear Algebra and Real Analysis. My video courses can help you there if you want to refresh your memory. Use them while watching the videos about distributions whenever you don’t understand a term we use. On the other hand, if you are interested in the topics about distributions, you might also be interested in my Functional Analysis and Measure Theory series. However, they are not necessarily needed to understand this course but still some videos could help you for getting more deep insights into the field of distributions.
Content of the video:
00:00 Intro
00:16 Analysis
01:30 Historical Example
03:55 Delta is not an ordinary function
06:10 Visualisation
8:00 Delta Function
9:20 Outro
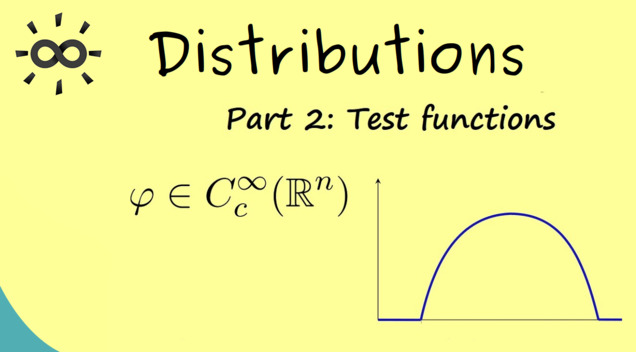
Part 2 - Test Functions
After this short historic overview, we can go into the mathematical definitions. We start by defining the so-called test functions:
Part 3 - Convergence of Test Functions
Now you know the space of test functions as a set. However, they have also some important properties, we should discuss. One that is immediately used is a notion of convergence.
Part 4 - Space of Distributions
At this point, we are ready to define the important space of distributions. It turns out that this is not so complicated when you are already familiar with linear maps.
Part 5 - Regular Distributions
Next, we look at more examples for distributions. Most importantly, we will define so-called regular distributions. This will be the starting point for a lot of definitions that will follow.
Part 6 - The Delta Distribution Is Not Regular
We have already introduced the famous delta distribution. Now, we can show that this is not a regular distribution.
Part 7 - Distributions Form a Vector Space
Let’s go one step back and look at the space we have defined. Distributions are linear functionals with an additional property: the particular continuity defined above. However, the space still, very naturally, forms a vector space. This means that we can add and scale distributions.
Part 8 - Multiplication with Smooth Functions
In the same way, we could define the multiplication of distributions. However, it turns out that, in general, the product of two distributions cannot be defined in the useful manner. Therefore, we restrict ourselves to the multiplication of a distribution with a smooth function.
Part 9 - Coordinate Transformation
Since we are working in the n-dimensional space $ \mathbb{R}^n $, coordinate transformations are very natural. The simplest ones, can be described by invertible linear maps. Let’s see how distributions should change under such transformations.
Part 10 - Distributional Derivative
This is one of the most important definitions for distributions: we will extend the classical definition of a derivative, which only holds for smooth functions, to the whole realm of distributions, which don’t have to be smooth at all. It turns out that this extension works for every distributions such that a lot of technical problems for differential equations are already solved with this.
Part 11 - Fundamental Solution
The next video is interesting for everyone who already learnt a little bit about partial differential equations. There one usually starts with an important example: the Laplace equation. For this is turns out that one has a so-called fundamental solution that helps constructing solutions for the inhomogeneous equation. By using distributions, in particular by using the delta distribution, one can put a rigourous meaning to this concept.
Part 12 - Finite-Order Distributions
The following video just wants to show a nice concept of some special distributions is not really needed for the rest of the series. However, it’s nice to see that some distributions coincide with ordinary measures as one learn about them in the Measure Theory series.
Part 13 - Convolution
In this video, we will first talk about the convolution as an operation for functions. Then we will also see how we can generalize this to get a convolution between test functions and distributions.
Part 14 - Convolution to Solve Partial Differential Equations
Now we go deeper in the study of the convolution. First let’s show that the delta distribution acts like a neutral element there.
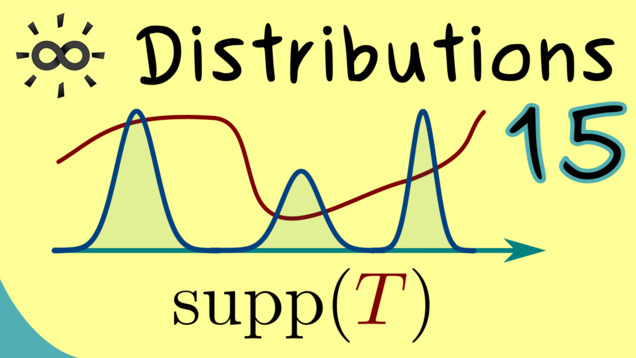
Part 15 - Support for Distributions
In order to generalize the definition of the convolutions even more, we first have to talk about the support for a distribution $T \in \mathcal{D}^\prime(\mathbb{R}^n)$. In short, it should describe at which points the distribution does not vanish. However, this requires some explanations about what this actually means because, in general, one cannot how a distribution acts on single points.
Part 16 - Distributions with Compact Support
Let’s define a subset of special distributions, denoted by $\mathcal{E}^\prime(\mathbb{R}^n)$. These are the distributions of compact support. It turns out that one can extend them to a bigger domain of definition, which we will also discuss here.
Part 17 - Convolution with Distributions of Compact Support
By using the special distributions of compact support, one can extend the definition of the convolution even more such that the convolution between two distributions makes sense.
Summary of the course Distributions
- You can download the whole PDF here and the whole dark PDF.
- You can download the whole printable PDF here.
- Test your knowledge in a full quiz.