Information about Linear Algebra - Part 46

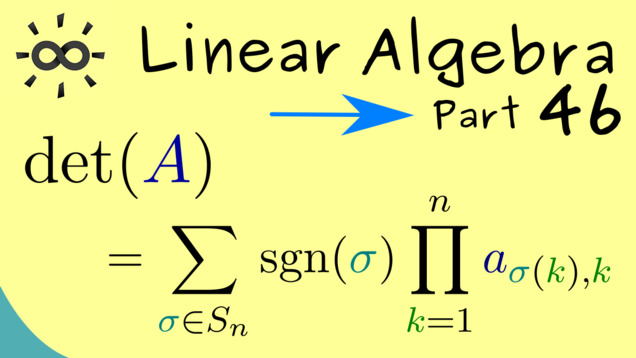
Title: Leibniz Formula for Determinants

Series: Linear Algebra

YouTube-Title: Linear Algebra 46 | Leibniz Formula for Determinants

Bright video: https://youtu.be/iClIgDt55lM

Dark video: https://youtu.be/2ddRZsBdzJc

Quiz: Test your knowledge

PDF: Download PDF version of the bright video

Print-PDF: Download printable PDF version

Thumbnail (bright): Download PNG

Back to overview page