Information about Linear Algebra - Part 40

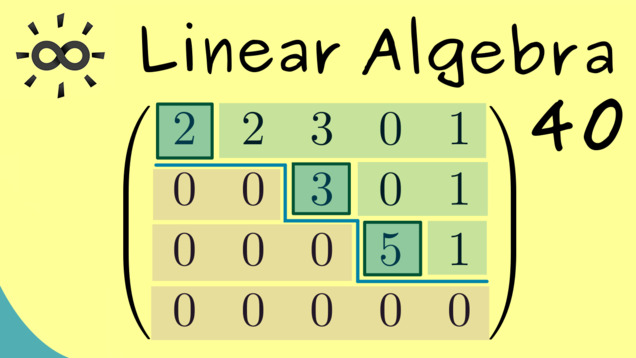
Title: Row Echelon Form

Series: Linear Algebra

YouTube-Title: Linear Algebra 40 | Row Echelon Form

Bright video: https://youtu.be/nRXt9zUNLK4

Dark video: https://youtu.be/kCp7cTwli0M

Quiz: Test your knowledge

PDF: Download PDF version of the bright video

Print-PDF: Download printable PDF version

Thumbnail (bright): Download PNG

Back to overview page