Here, you find my whole video series about Ordinary Differential Equations in the correct order and I also help you with some text around the videos. If you want to test your knowledge, please use the quizzes, and consult the PDF version of the video if needed. When you have any questions, you can use the comments below and ask anything. However, without further ado let’s start:
Part 1 - Introduction
Ordinary Differential Equations is a video series I started for everyone who is interested in the theory of differential equations and dynamics and also in concrete solution methods.:

With this you now know the topics that we will discuss in this series. Now, in the next video let us discuss definitions in the topic.
Part 2 - Definitions
There are a lot of notions one has to define to get a precise definition what a differential equation is and what it means to find solutions for it. Let’s do it:

Part 3 - Directional Field
After defining all these new manners of speaking, we are ready to go to a more visual approach. The direction field is essentially just a graph visualisation of a vector-valued function but it helps a lot to get properties from a given differential equation. We will first look at one- and two-dimensional examples.

Part 4 - Reducing to First Order
We already used it in the last video: the fact that every ordinary differential equations could be described as a system of first order. Now we will fill in these gaps and show the correct substitutions, one needs to get this result.

Part 5 - Solve First-Order Autonomous Equations
In this video, we will consider a general one-dimensional differential equation of first order. It turns out that we can describe the solution just as an antiderivate.

Part 6 - Separation of Variables
Now, we are ready to generalise the result from the last video. We can do that in a special situation when two variables can be separated.

Part 7 - Solving Linear Equations of First Order
In this video, we learn about the method of integrating factor to solve linear ODEs. This is equivalent to the method of variation of the constant, which is often taught in this context.

Part 8 - Existence and Uniqueness?
In this video, we start discussing if solutions of initial value problems can exist and if we even find uniquness. By looking at the directional field, we conclude that existence should be given but uniqueness is not garantueed. However, we will give sufficient conditions for unique solutions in future videos.

Part 9 - Lipschitz Continuity
Now, we will look at so-called Lipschitz-continuous functions. They lie, in some sense, between continuously differentiable and continuous functions. It turns out that they give a sufficient criterion for having unique solutions of an initial value problem.

Part 10 - Uniqueness for Solutions
Now we are ready to prove the uniqueness of a solution for a given initial value problem if a Lipschitz condition is satisfied.

Part 11 - Banach Fixed Point Theorem
In order to show the existence for initial value problem, we can use a general result from analysis. This is an important fixed point theorem which can be proven just by just using some knowledge of convergent sequences and complete spaces. However, I don’t want to show proof but how to apply to ordinary differential equations.
If you want to learn how to proof this important theorem, you can check out the supplementary video about the Banach fixed-point theorem.
Part 12 - Picard–Lindelöf Theorem
Finally, we can state the famous Picard–Lindelöf Theorem, which summarizes existence and uniqueness for an inital value problem assuming the corresponding vector field is Lipschitz-continuous.

Part 13 - Picard Iteration
The proof of the Picard–Lindelöf Theorem used the Banach fixed-point theorem. However, this one comes with an interation formula for approximating the fixed-point. It’s a general result and therefore also useful in the theory of ordinary differential equations. Indeed, we can start with an approximation of the solution for an initial-value problem and then we can improve it step by step. In the limit we get the actual unique solution. This whole procedure, which only includes integration, is known as the Picard iteration.
Part 14 - Maximal and Global Solutions
Now, we have to get more technical. For always talked about uniqueness in the local sense. We just showed that in a small neighbourhood the solution of an initial value problem has to be unique. However, how is it in a global sense? Can we extend this local behaviour to a larger domain? To answer this, we have to define the notions maximal solution and global solution.
Part 15 - Phase Portrait
Before we already mentioned the phase space for an ordinary differential equation. We could sketch the directional field for a system $ \dot{x} = v(x) $ and also so-called orbits. Now, the collection of all these orbits gets a special: we call it the phase portrait. For locally Lipschitz continuous vector field, we have the result that orbits fill out the whole picture and that two orbits cannot cross each other.
Part 16 - Periodic Solutions and Fixed Points
Let’s look at some special orbits we find in the phase potrait: fixed points and periodic solutions. To visualize these special solutions, let’s consider the mathematical pendulum given by the ordinary differential equation $ \ddot{x} = - \sin(x) $.
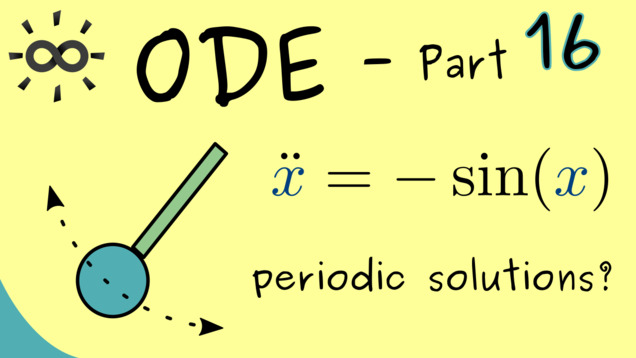
Part 17 - Picard–Lindelöf Theorem (General and Special Version)
Let’s revisit the Picard-Lindelöf theorem again. We can generalize the claim to non-autonomous systems where we only need a suitable Lipschitz condition in the space-variable, and we can also specify the theorem if we have a global Lipschitz condition instead of a local one. In the last case, we can prove the existence of global solutions.

Part 18 - System of Linear Differential Equations
In part 7, we already discussed how to solve linear differential equations, but this was restricted to the one-dimensional case. So it’s a natural question to ask if one can generalize this whole procedure to an $n$-dimensional system. This is one is written as $\dot{x} = A(t) x + b(t)$ where $ A(t) \in \mathbb{R}^{n \times n} $.

Part 19 - Solution Space
Let’s consider the homogenous part of system of linear ODEs. For this, we can prove that the set of solutions forms a vector space. Moreover, we are also able to calculate the dimension of this solution space.

Part 20 - Matrix Exponential
It turns out that we can make sense of $e^A$ where $A$ is matrix. This generalizes the idea of finding solution for a one-dimensional ODE of the form $ \dot{x} = a x $, where the solution space is spanned by $ t \mapsto e^{a t} $. In this video, we will show that, for a homogeneous and autonomous system $ \dot{x} = A x $, the solution space is also spanned by the columns of the matrix $ e^{t A} $.

Part 21 - Solution Set of Linear ODEs
To generalize the discussions from the last videos, we can finally explain how the solution set for a general system of linear ODEs looks like. It turns out that the homogenous part contains almost already all information.

Part 22 - Properties of the Matrix Exponential
We’ve already seen that the matrix exponential represents the solution set of an autonomous linear ODE. Therefore, it’s important that we know how to calculate with an expression like $e^{t A}$. In particular, we want to know what the derivative of the function $t \mapsto e^{t A}$ is and when the formula $e^{A+B} = $e^{A} \cdot e^{B} $ holds.
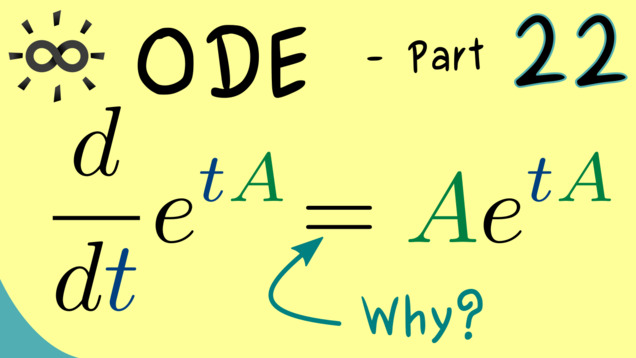
Part 23 - Example for Matrix Exponential
After a lot of theoretical discussions, we can finally look at an explicit calculation of a matrix exponential to solve a system of linear differential equations. The important thing is that we have an autonomous system such we can easily calculate the matrix exponential. It turns out that, in particular for diagonalizable matrices, this construction is straightforward. One just has to determine eigenvalues and eigenvectors to calculate all the powers of the given matrix $A$.

Part 24 - Characteristic Polynomial
Let’s look at higher order ODEs again. In particular, linear differential equations can be solve with our method from first order systems, which means by using the matrix exponential. There, we already know that the key ingeredient is given by eigenvalues and therefore by the zeros of the characteristic polynomial. It turns out that we can also directly define it for a linear differential equation of order $n$.

Summary of the course Ordinary Differential Equations
- You can download the whole PDF here and the whole dark PDF.
- You can download the whole printable PDF here.
- Ask your questions in the community forum about Ordinary Differential Equations
Ad-free version available:
Click to watch the series on Vimeo.