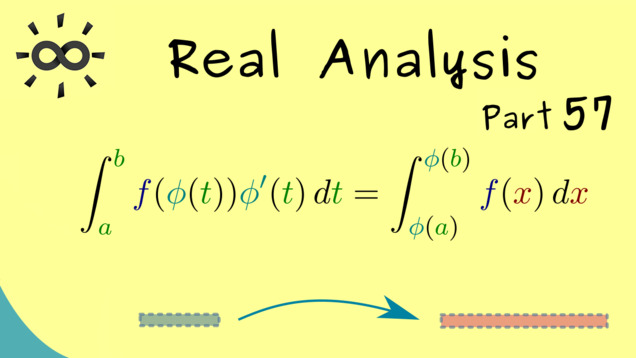
-
Title: Integration by Substitution
-
Series: Real Analysis
-
Chapter: Riemann Integral
-
YouTube-Title: Real Analysis 57 | Integration by Substitution
-
Bright video: Watch on YouTube
-
Dark video: Watch on YouTube
-
Ad-free video: Watch Vimeo video
-
Original video for YT-Members (bright): Watch on YouTube
-
Original video for YT-Members (dark): Watch on YouTube
-
Forum: Ask a question in Mattermost
-
Quiz: Test your knowledge
-
Dark-PDF: Download PDF version of the dark video
-
Print-PDF: Download printable PDF version
-
Exercise Download PDF sheets
-
Thumbnail (bright): Download PNG
-
Thumbnail (dark): Download PNG
-
Subtitle on GitHub: ra57_sub_eng.srt missing
-
Download bright video: Link on Vimeo
-
Download dark video: Link on Vimeo
-
Related videos:
-
Timestamps (n/a)
-
Subtitle in English (n/a)
-
Quiz Content
Q1: Let $f,\phi: \mathbb{R} \rightarrow \mathbb{R}$ be two continuously differentiable functions. What is the correct substitution rule?
A1: $ \displaystyle \int_a^b f(x) dx $ $ \displaystyle= \int_{\phi(a)}^{\phi(b)} f(t) dt $
A2: $ \displaystyle \int_{\phi(a)}^{\phi(b)} f(x) dx $ $ \displaystyle = \int_{\phi(a)}^{\phi(b)} f(t) dt $
A3: $ \displaystyle \int_{\phi(a)}^{\phi(b)} f(x) dx $ $ \displaystyle = \int_{a}^{b} f(t) \phi^\prime(t) dt $
A4: $ \displaystyle \int_{\phi(a)}^{\phi(b)} f(x) dx $ $ \displaystyle = \int_{a}^{b} f(\phi(t)) \phi^\prime(t) dt $
A5: $ \displaystyle \int_{\phi(a)}^{\phi(b)} f(x) dx $ $ \displaystyle = \int_{a}^{b} f(\phi(t)) dt $
Q2: What is the antiderivative of the function $f:\mathbb{R} \rightarrow \mathbb{R}$ given by $$f(t) = t^4 \cos(t^5),.$$
A1: $ \displaystyle \sin(t) $
A2: $ \displaystyle -\frac{1}{5} \sin(t^5) $
A3: $ \displaystyle \frac{1}{5} \cos(t^5) $
A4: $ \displaystyle \frac{1}{5} \sin(t^5) $
Q3: What is the integral $ \displaystyle \int_0^1 t \exp(t^2) , dt$?
A1: $0$
A2: $\frac{1}{2} e - 1$
A3: $\frac{1}{2} (e - 1)$
A4: $\frac{1}{2} (e - 2)$
A5: $\frac{1}{3} (e - 1)$
-
Last update: 2025-09
