Here, you find my short advent calender about mathematical symbols. Each video introduces a symbol that one uses in mathematics. You can also download the pdf versions of the videos here.
Part 1 - Kronecker Delta
The first video is about the Kronecker Delta:

Part 2 - Levi-Civita Symbol
Let’s continue with the related Levi-Civita Symbol, which can be used to describe the cross product in $ \mathbb{R}^3 $.

Part 3 - Nabla-symbol
The next symbol is called Nabla and used for partial derivatives. We find the notation is the my video series about multivariable calculus again where we talk about gradients and directional derivatives.

Part 4 - Factorial
In the following video, we explain the common Factorial notation. It is used in a lot of mathematical contexts.
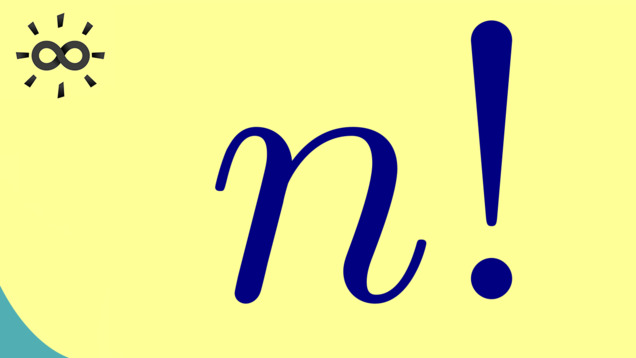
Part 5 - Gamma Function
The Gamma Function is a generalisation of the last video:

Part 6 - Composition
For denoting the composition for functions, we use a special symbol:

Part 7 - Sum Symbol
The capital sigma we use to denote the sum symbol:

Part 8 - Product Symbol
Moreover, the Greek capital Pi is used for the product symbol:

Part 9 - Restriction
Do you know the symbol for the restriction of a function?

Part 10 - Pauli matrices
Some matrices you see in physics a lot: Pauli matrices.

Part 11 - Set Brackets
Naturally a fundamental notation: set brackets.

Part 12 - Big O
The Big O notation is used in a lot of formulas.

Part 13 - Binomial Coefficient
Next, we look at the binomial coefficient

Part 14 - Modulo
The modulo notation is important when you work with numbers.

Part 15 - Beta Function
The next video is about the Beta function.

Part 16 - Map Arrows
Also a fundamental notation is given by the map arrows. This is a notation that is used throughout mathematics. Please note that different arrows are used for the different levels.

Part 17 - Little o
For some formulas the Little o notation is helpful.

Part 18 - Outer Product
Next, let’s discuss the outer product. This is a special symbol, which is also used in other contexts. However, the outer product is the simplest one of the usages.

Part 19 - Euler’s Phi Function
Are you interested in Euler’s Phi Function

Part 20 - Laplace Operator
The Laplace operator a very important object in differential equations. It is given by second-order partial differential operators.

Part 21 - Convolution
Next symbol ist about the convolution

Part 22 - Heaviside Function
Do you know the Heaviside function? It is a function that has one heavy side but the name comes from the famous mathematician Heaviside.

Part 23 - Quaternions
Let us talk about quaternions.

Part 24 - Infinity
And finally the last video in this series is about infinity. A symbol that is used for a lot of different contexts. However, one can also calculate with it, in some sense.

Part 25 - Element Symbol
This is one of the most often used symbols in mathematics. It originated from a lowercase epsilon and it simply describes the set-element relation.

Part 26 - Empty Set
Talking about sets: there is a very special set that just describes nothingness.

Part 27 - Subset Symbol
In mathematics, we imagine that sets are collections of objects and such collections can be compared. The usual and natural way is to do that with the subset notation.

Part 28 - Partial d
The next symbol is very special one. It does not use a character from an alphabet but is somehow a deformed d or lowercase delta. It’s always used to denote partial derivatives such one common name is partial d but a lot of people call it and pronouce it del.

Part 29 - D’Alembert Operator
This symbol looks like a box and it’s often used in physics and in mathematics for partial differential equations.

Part 30 - Inner Product
This is an important construction for giving a geometry to different spaces. Especially in Quantum Mechanics, this notation got popular.

Part 31 - Integral Symbol
Ah, the integral symbol. One of the symbols that really calls for a mathematician. However, essentially, it’s just a stylized S but now with a lot of meaning in different fields of mathematics.

Part 32 - Closed Line Integral
This is a special notion for an integral that is often used in complex analysis and vector analysis.

Part 33 - Natural Numbers
If you start learning mathematics, you immediately learn about sets and the set of natural numbers is the first infinite set in this introduction.

Part 34 - Integers
Let’s finish this series with integers, a set that shows that even an infinite set as the natural numbers can be extended in a natural way.

Summary of the course Advent of Mathematical Symbols
- You can download the whole PDF here and the whole dark PDF.
- You can download the whole printable PDF here.
- Test your knowledge in a full quiz.
- Ask your questions in the community forum about Advent of Mathematical Symbols
Ad-free version available:
Click to watch the series on Vimeo.