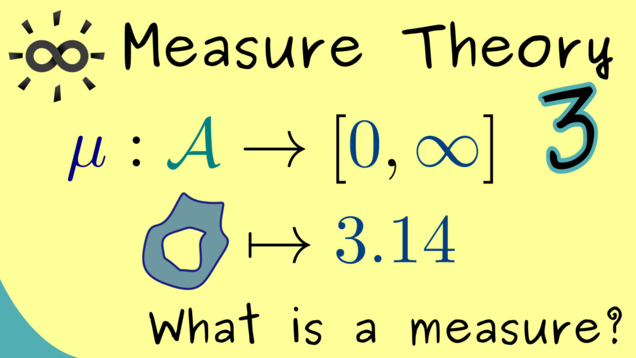
-
Title: What is a measure?
-
Series: Measure Theory
-
YouTube-Title: Measure Theory 3 | What is a measure?
-
Bright video: https://youtu.be/7O7qPrNIt7w
-
Dark video: https://youtu.be/GHdBo2uKfiM
-
Ad-free video: Watch Vimeo video
-
Quiz: Test your knowledge
-
Dark-PDF: Download PDF version of the dark video
-
Print-PDF: Download printable PDF version
-
Thumbnail (bright): Download PNG
-
Thumbnail (dark): Download PNG
-
Subtitle on GitHub: mt03_sub_eng.srt
-
Other languages: German version
-
Timestamps
00:00 Introduction
00:26 Measure - Definition
03:08 Empty set has measure zero
03:35 Additivity
05:59 Sigma-additivity
07:54 Summary
08:43 Measure space
09:18 Examples
09:40 Counting measure
12:30 Dirac measure
14:12 Lebesgue measure
-
Subtitle in English
1 00:00:00,060 –> 00:00:08,220 Hello and welcome back to measure theory. This is part 3 and today we will finally start talking
2 00:00:08,220 –> 00:00:14,340 about what measure is. I will start talking about the definition and then I explain you
3 00:00:14,340 –> 00:00:21,870 all the details. Afterwards then I can show you some examples for measures. To summarize in this
4 00:00:21,870 –> 00:00:28,590 video the question would be: what is a measure? To answer this question let’s immediately start
5 00:00:28,590 –> 00:00:36,750 with the definition. What we need is a set X and a sigma-algebra on the set X and let’s call this
6 00:00:36,750 –> 00:00:44,220 Sigma Algebra just A. And such a pair is then just called a measurable space. So nothing special,
7 00:00:44,220 –> 00:00:51,750 it just means you have a set X and you fixed one Sigma algebra on this set. And by now you know
8 00:00:51,750 –> 00:00:59,910 that a sigma algebra is a special collection of subsets of this set X. Now we will look at special
9 00:00:59,910 –> 00:01:09,060 maps that are defined on the Sigma algebra A. And such map I will always call by our lowercase mu.
10 00:01:09,060 –> 00:01:17,580 So it’s defined on the Sigma A and maps into the positive real numbers. However we include
11 00:01:17,580 –> 00:01:26,040 some small detail: on the one side we include 0, so 0 is allowed, and then we go to infinity, so
12 00:01:26,040 –> 00:01:33,060 this would be our normal interval: so we just look at a positive real line including 0. But here in
13 00:01:33,060 –> 00:01:39,630 the measure theory, we will change this a little bit we also include infinity. OK, this might look
14 00:01:39,630 –> 00:01:46,710 a little bit strange, and it is, because we just include one new symbol, so this means, we have our
15 00:01:46,710 –> 00:01:54,210 positive real line where we include the 0, so this is normal, but we also include a new symbol and we
16 00:01:54,210 –> 00:02:01,230 just call this symbol infinity. And to shorten this notation, we just write here also infinity
17 00:02:01,230 –> 00:02:08,580 is included in the interval. This means that it is just a short notation for saying that we have also
18 00:02:08,580 –> 00:02:16,450 a symbol infinity involved. How to calculate with this new symbol, I tell you later. First I want to
19 00:02:16,450 –> 00:02:23,680 tell you how such a map is now called. Maybe not so surprising such a map is now called a measure.
20 00:02:23,680 –> 00:02:31,750 However only if the following two conditions are fulfilled. To see what these two rules should be,
21 00:02:31,750 –> 00:02:40,570 maybe recall what we want. We want to measure subsets of this set X, which means we want to
22 00:02:40,570 –> 00:02:48,820 give a volume to such a subset. So a generalized length or generalized volume. Therefore makes
23 00:02:48,820 –> 00:02:54,670 totally sense to restrict ourselves to the positive real numbers where we also include zero
24 00:02:54,670 –> 00:03:01,660 and the symbol infinity; which means we could also have a volume of zero and maybe also an infinite
25 00:03:01,660 –> 00:03:09,460 volume. But all other volumes should be positive numbers. From this, we immediately get our first
26 00:03:09,460 –> 00:03:17,440 property because we know that the empty set is a subset of X and in all Sigma algebras A involved.
27 00:03:17,440 –> 00:03:24,340 Therefore we want to measure this empty set or we want to give it a volume. But the only sensible
28 00:03:24,340 –> 00:03:33,190 volume we can give the empty set would be zero. If there are no elements involved, the generalized
29 00:03:33,190 –> 00:03:39,760 volume should be zero. Okay for the start not so complicated so let’s go to our second property,
30 00:03:39,760 –> 00:03:48,520 this property should fix the idea that we can add up volumes. Or in other words, if we have
31 00:03:48,520 –> 00:03:58,750 a subset given (so maybe just in this rectangle), then we could split it up into subsets (so maybe
32 00:03:58,750 –> 00:04:10,060 in this way maybe here line and here line). So I would call this A1, this is A2, this A3, A4, and
33 00:04:10,060 –> 00:04:19,600 A5. Now if we add up all these separate volumes, we should end at our original volume. And this
34 00:04:19,600 –> 00:04:26,470 is the condition I can write down. So adding up all the volumes where we start with i equals to 1
35 00:04:26,470 –> 00:04:33,910 and we’ll end with five, or we just write an N in this generality. So we’re adding up the volumes,
36 00:04:33,910 –> 00:04:43,000 which means I add up mu of A_i. And we also know, we chose the sets to be disjoint, pairwise
37 00:04:43,000 –> 00:04:50,890 disjoint, because we want a decomposition of our original set. Pairwise disjoint means now that
38 00:04:50,890 –> 00:05:00,760 A_i intersected with A_j is the empty set if the indices do not coincide. So i is not equal to j.
39 00:05:00,760 –> 00:05:07,660 Now you see something’s missing in our condition but we can fix that immediately because we know
40 00:05:07,660 –> 00:05:16,630 this should be the original volume. So I can write this as the volume of the union of all these sets.
41 00:05:16,630 –> 00:05:26,950 So I write here i equals to one going to N and here I have my A_i. This is the union that gives
42 00:05:26,950 –> 00:05:34,480 us indeed our original green set here. And this condition should be satisfied no matter which
43 00:05:34,480 –> 00:05:43,600 sets we chose. So I just write this should hold for all A_i out of our Sigma algebra. And this
44 00:05:43,600 –> 00:05:51,100 property is what one calls just additive. It tells you that if you have a finite union, you can split
45 00:05:51,100 –> 00:05:59,200 that up into a finite sum of the volumes. However I should tell you, this is not the full story. We
46 00:05:59,200 –> 00:06:06,190 also want to include the intuition that we can also approximate volumes. Maybe I explain it
47 00:06:06,190 –> 00:06:11,830 again in the picture. So if you want to calculate the volume of this rectangle, we can split it up
48 00:06:11,830 –> 00:06:23,080 again into subsets so this is my set A_1. Then I also choose an A_2 here and A_3 here and then I go
49 00:06:23,080 –> 00:06:32,350 on and on. So this would be my A_4 and A_5 and you see I get smaller and smaller. But you see
50 00:06:32,350 –> 00:06:41,320 I get again the decomposition of my original set into disjoint subsets. However, I have infinitely
51 00:06:41,320 –> 00:06:49,150 many subsets now. But they are countable, which means I have a sequence of subsets. Now you know,
52 00:06:49,150 –> 00:06:57,970 I can still form the union of all the subsets to get out my original set. Which means I put in here
53 00:06:57,970 –> 00:07:06,910 an infinity symbol to denote this union. And if I add up the infinitely many unions, I should
54 00:07:06,910 –> 00:07:14,560 also get out the original volume. So instead of a finite sum, I have now a series here; but it’s
55 00:07:14,560 –> 00:07:22,180 the series of non-negative numbers. Therefore to denote this countable infinite additive rule, we
56 00:07:22,180 –> 00:07:30,070 usually call it sigma additive. And please recall we had the same idea in the definition of the
57 00:07:30,070 –> 00:07:37,180 Sigma algebra: we want this union, this countable infinity union, also be in the Sigma algebra. And
58 00:07:37,180 –> 00:07:43,240 therefore this is also well-defined because if we choose elements from the Sigma algebra, we know
59 00:07:43,240 –> 00:07:49,360 that this countable union is also in a sigma algebra. Therefore we can calculate mu of this
60 00:07:49,360 –> 00:07:56,620 one. And now we have it this is the definition of a measure. Maybe let’s summarize that:
61 00:07:56,620 –> 00:08:04,030 a measure has to live on a Sigma algebra. It does not have to be the whole power set (it could be),
62 00:08:04,030 –> 00:08:09,940 but in general we will see we can’t do it for the whole power set. This just means that we
63 00:08:09,940 –> 00:08:17,230 want to measure some meaningful subsets from our set X. Measuring subsets now means giving them
64 00:08:17,230 –> 00:08:23,890 a generalized volume, so it makes sense to give them a volume in the non-negative numbers where
65 00:08:23,890 –> 00:08:30,700 we also include a symbol infinity. And then the two properties generalize the ideas from a volume
66 00:08:30,700 –> 00:08:38,080 measure. The first thing tells you nothing should have a zero volume and the second tells you that
67 00:08:38,080 –> 00:08:45,820 you can calculate the volume by splitting it up into countable many subsets. Now let’s assume you
68 00:08:45,820 –> 00:08:53,430 have a measure chosen, then we can also fix that in our informations here. You would write X with
69 00:08:53,430 –> 00:09:00,690 the Sigma algebra A and with our measure on the Sigma algebra A: mu. And this is what we call a
70 00:09:00,690 –> 00:09:07,920 measure space. This is of course a very important notion because the measure space is the space we
71 00:09:07,920 –> 00:09:15,150 work in. Very good. Now you learned what such a general measure space is. And now we can talk
72 00:09:15,150 –> 00:09:24,570 about some simple examples. Let us fix for all the examples, an arbitrary set X and also a Sigma
73 00:09:24,570 –> 00:09:30,120 algebra on the set X. And maybe we start with the best case scenario that we can choose the whole
74 00:09:30,120 –> 00:09:38,760 power set for the Sigma algebra. The first measure is very important and very easy, it’s called the
75 00:09:38,760 –> 00:09:45,450 counting measure. No matter what set X is, you can always define this counting measure. Simply
76 00:09:45,450 –> 00:09:53,130 by setting that the measure of an arbitrary subset a is defined in the following way and I consider
77 00:09:53,130 –> 00:10:01,050 two cases here. The first case would be that A has only finitely many elements. In this case,
78 00:10:01,050 –> 00:10:07,410 I want the measure to be this number, so I can just write down the number of elements just by the
79 00:10:07,410 –> 00:10:14,250 number symbol. So this is a well-defined natural number or zero. So we don’t have a problem,
80 00:10:14,250 –> 00:10:21,510 defining exactly this. Okay for the other case, I set it to infinity. Which means if A has not
81 00:10:21,510 –> 00:10:28,830 finitely many elements, I say it has infinitely many elements. There you see: it makes sense to
82 00:10:28,830 –> 00:10:35,520 use our symbol infinity. What you can now show is that this defines really a measure, so it fulfills
83 00:10:35,520 –> 00:10:41,490 these two rules. So that the empty set gets sent to zero is immediately clear because the empty
84 00:10:41,490 –> 00:10:48,480 set has finitely many elements and the number of elements is zero. So no problem there and also
85 00:10:48,480 –> 00:10:55,470 the Sigma additivity, you can easily show if you just deal with finite sets. If you deal with the
86 00:10:55,470 –> 00:11:01,140 infinite sets, it’s also easy to show but then you need to know what are the calculations rules when
87 00:11:01,140 –> 00:11:08,890 I deal with this infinity symbol. And this is what I now want to show you. So just the basic
88 00:11:08,890 –> 00:11:14,980 calculation rules. The idea is of course thinking in the volumes. So if you have one volume x,
89 00:11:14,980 –> 00:11:22,810 and then you add up an infinite volume (so you add up infinity), you also should get out to infinity
90 00:11:22,810 –> 00:11:30,640 again. And this should hold for all x in our set. So also for the symbol infinity. Or other words
91 00:11:30,640 –> 00:11:36,910 infinity plus infinity is always infinity. In the same way we can do this for the multiplication:
92 00:11:36,910 –> 00:11:46,270 so x times infinity should be also defined as infinity. However now be careful, I want to
93 00:11:46,270 –> 00:11:54,130 exclude 0 now. So if I multiply a positive number with infinity, we get out to infinity again, but
94 00:11:54,130 –> 00:12:01,840 not for 0. For the special case 0 times infinity, there are different conventions. In general, you
95 00:12:01,840 –> 00:12:08,140 would just say this is undefined because it could mean anything. However in most cases in measure
96 00:12:08,140 –> 00:12:14,380 theory, it’s also nice to have a definition for this combination of the symbols, and we
97 00:12:14,380 –> 00:12:22,000 set it to 0. However keep in mind, this is not always applicable and, outside of measure theory,
98 00:12:22,000 –> 00:12:29,620 it could be completely wrong. Often this occurs if we want to multiply two volumes. Then let’s
99 00:12:29,620 –> 00:12:37,030 go to the next example and this one is called the Dirac measure. Maybe for this one visualize your
100 00:12:37,030 –> 00:12:47,560 set X here where we choose one fixed point, so we choose here maybe a point p inside X. And now we
101 00:12:47,560 –> 00:12:54,010 just want that the whole measure is concentrated in only this point. The usual notation one chooses
102 00:12:54,010 –> 00:13:01,540 for this measure is a delta where we have an index p to denote the point. Now for a given subset A,
103 00:13:01,540 –> 00:13:11,770 we also define it with two cases. It is either 1 or 0. The idea we could also sketch in our drawing
104 00:13:11,770 –> 00:13:19,810 here. So if this is our set A, we see that p is inside the set A. And if we want to volume to be
105 00:13:19,810 –> 00:13:26,680 concentrate at the point p, we now would say: okay this set has measure 1. So it doesn’t matter how
106 00:13:26,680 –> 00:13:34,630 small the set is. As long as the special point p is inside, it has measure 1. But if P is not
107 00:13:34,630 –> 00:13:41,320 inside the set, then it has measure 0. A good visualization would be to think of this point as
108 00:13:41,320 –> 00:13:48,190 a point charge. The whole charge is in the point but if you look at the surrounding you would give
109 00:13:48,190 –> 00:13:55,900 also the surrounding exactly this charge. Okay so these were two measures that work on every set X,
110 00:13:55,900 –> 00:14:05,050 so in particular also for our special case R^n. Or in other words these measures don’t measure
111 00:14:05,050 –> 00:14:13,660 the normal volume you, for example, have in R^3. They are indeed generalized measures. But we know
112 00:14:13,660 –> 00:14:20,770 we also want to have this normal volume measure in R^n. Therefore the exercise for measure theory is
113 00:14:20,770 –> 00:14:30,280 in particular to find a measure on X equal to R^n that has some nice properties. The first property
114 00:14:30,280 –> 00:14:37,570 would fix that it measures the normal volume. This means that if I put in the unit cube in
115 00:14:37,570 –> 00:14:45,040 the measure, which is a cube that has length 1 in all directions, then I want to get out the volume
116 00:14:45,040 –> 00:14:52,660 1 as well. And the second property means it does not matter where we measure the volume in space.
117 00:14:52,660 –> 00:15:01,510 In other words, the measure is invariant under translations. So I can write that as x plus our
118 00:15:01,510 –> 00:15:10,780 set A is equal to the volume of the set A. And this holds for all translation vectors x in R^n.
119 00:15:10,780 –> 00:15:19,690 Also visualize always this property in a short picture. If you have your volume here so maybe
120 00:15:19,690 –> 00:15:27,460 this might be the set A. And now I translate all the points with a fixed vector x. Then I find the
121 00:15:27,460 –> 00:15:36,600 new set x plus A here. So this is my set x plus A. And of course this should have the same volume in
122 00:15:36,600 –> 00:15:43,890 our surrounding space. Of course this is not true for an abstract generalized measure from before.
123 00:15:43,890 –> 00:15:49,800 But it should be true for our measure that we want to find that generalizes the normal volume
124 00:15:49,800 –> 00:15:57,990 measure in R^n. However keep in mind: we only know how to measure such cubes or cuboids and not how
125 00:15:57,990 –> 00:16:04,230 to measure such an arbitrary subset. And that’s the idea that we want to extend this notion and
126 00:16:04,230 –> 00:16:11,670 still conserve these two properties. Later we will see that we can indeed define a measure with this
127 00:16:11,670 –> 00:16:17,550 two properties and that is what we then call the Lebesgue measure. And in the next video you will
128 00:16:17,550 –> 00:16:25,020 see that we can’t choose the whole power set as a sigma-algebra. We have to choose a smaller one
129 00:16:25,020 –> 00:16:32,070 such that we can conserve these two properties. And there you will see that we can easily work in
130 00:16:32,070 –> 00:16:38,940 the Borel sigma-algebra. Well very good. That’s all I wanted to tell you today and I hope that
131 00:16:38,940 –> 00:16:45,750 helped you a little bit. For the next videos, the real measure theory can start because now we
132 00:16:45,750 –> 00:16:53,220 have the notion what a measure and a measure space is. So thank you very much and see you next time!
-
Quiz Content
Q1: Is $\mu: \mathcal{P}(\mathbb{R}) \rightarrow \mathbb{R}$ with $\mu(A) = 0$ for all sets $A$ a measure?
A1: Yes, it is.
A2: No, one property is not satisfied.
Q2: Let $\mu: \mathcal{P}(\mathbb{N}) \rightarrow \mathbb{R}$ be the counting measure. Calculate $\mu( { 1,2,2,4 } ) $.
A1: 1
A2: 2
A3: 3
A4: 4
A5: 5
Q3: Let $\delta_2: \mathcal{P}(\mathbb{N}) \rightarrow \mathbb{R}$ be the Dirac measure for point $2 \in \mathbb{N}$. Calculate $\delta_2( { 1,2,2,4 } ) $.
A1: 0
A2: 1
A3: 2
A4: 3
A5: 4
A6: 5
-
Last update: 2024-10