00:00 Recap sigma algebra

00:50 Intersections of sigma algebra

02:18 Generated sigma algebra

04:38 Example

08:30 Definition Borel sigma algebra

1 00:00:00,120 –> 00:00:03,000 Welcome back to measure theory.

2 00:00:03,186 –> 00:00:08,229 This is part 2 today and we still have to talk a little bit about sigma algebras.

3 00:00:09,071 –> 00:00:12,143 Here you can see the definition from last time.

4 00:00:12,330 –> 00:00:22,069 In short maybe a sigma algebra is just a family of subsets of a given set X, which fulfills these 3 rules.

5 00:00:22,400 –> 00:00:27,614 Which means the empty set and the full set is always in the sigma algebra

6 00:00:28,189 –> 00:00:32,657 and for each set also the complement is in the sigma algebra

7 00:00:32,943 –> 00:00:39,457 and the third rule says that you can form arbitrarily countable unions inside the sigma algebra.

8 00:00:40,143 –> 00:00:45,986 and all sets that are elements in the sigma algebra are just called measurable sets.

9 00:00:46,219 –> 00:00:53,214 Ok, that is good enough for a short recap and now I can tell you, it’s easy to show the following.

10 00:00:53,600 –> 00:00:58,471 Imagine you have a lot of different sigma algebras on a given set X.

11 00:00:59,186 –> 00:01:05,686 Let’s call them A_i, where i comes from an arbitrary index set.

12 00:01:06,129 –> 00:01:09,714 Here it does not matter if the index set is countable or not.

13 00:01:09,914 –> 00:01:15,900 What we can do then is, look at all the intersections of the sigma algebras.

14 00:01:16,571 –> 00:01:24,286 This is written in the following way. So this big cap, where we go over the index set and form the intersection.

15 00:01:24,429 –> 00:01:33,486 Now, as I said this is easy to show and I advice you to try it, that this indeed gives you again a sigma algebra.

16 00:01:34,229 –> 00:01:41,986 So it does not matter if you just look at the intersection of 2 sigma algebras or of the intersection of a lot of sigma algebras

17 00:01:42,171 –> 00:01:48,571 You still get the result, that you get a new, smaller sigma algebra from our set X.

18 00:01:49,443 –> 00:01:56,529 This result is very helpful if you want to have a lot of properties that your measurable set should have.

19 00:01:56,729 –> 00:02:05,914 Then you can just put the properties in different A_i’s and then just form an INTERSECTION to get out a sigma algebra,

20 00:02:06,043 –> 00:02:09,229 where all your measurable sets, have all the properties.

21 00:02:09,886 –> 00:02:17,057 In short this result helps you a lot, if you want to define a suitable sigma algebra for your problem

22 00:02:17,629 –> 00:02:25,771 and this gives rise to the next definition. For this let’s fix a family of subsets.

23 00:02:25,871 –> 00:02:30,579 So we have a subset of the power set of the given set.

24 00:02:30,971 –> 00:02:38,257 In other words just the collection of some subsets, which means they don’t have to form a sigma algebra yet.

25 00:02:39,286 –> 00:02:44,757 However the result is now that we can form a sigma algebra out of this M

26 00:02:45,014 –> 00:02:54,314 and we can choose the smallest sigma algebra and smallest just means with respect to the set inclusion, that contains this set M.

27 00:02:54,486 –> 00:02:59,614 The interesting thing is that we immediately know how to form such a small sigma algebra.

28 00:03:00,129 –> 00:03:02,971 Yeah, we just look at the intersection again.

29 00:03:03,071 –> 00:03:12,843 There we just put in sigma algebras A, where we know that our sigma algebra has to be bigger than our set M.

30 00:03:13,429 –> 00:03:21,271 Still, keep in mind that we are working inside the power set. So we are working with sets of subsets.

31 00:03:21,357 –> 00:03:27,157 That could be confusing, but it does not matter in our whole set construction here.

32 00:03:27,514 –> 00:03:31,557 Yeah and keep in mind that our A has to be sigma algebras.

33 00:03:34,986 –> 00:03:42,719 So we are putting in sigma algebras and use intersections so we know that something comes out and it is still a sigma algebra

34 00:03:42,871 –> 00:03:50,743 and because it’s an intersection of the smallest sigma algebra with this property. So the smallest one that contains M.

35 00:03:51,100 –> 00:03:54,343 However you see this is a long term to write down.

36 00:03:54,486 –> 00:04:04,743 Therefore the common notation one uses is just a sigma of this set M as the definition of this intersection.

37 00:04:05,414 –> 00:04:12,557 Another name for this sigma algebra is often the sigma algebra that is generated by M.

38 00:04:12,786 –> 00:04:20,657 Keep in mind, it’s no problem to find a sigma algebra that contains M. You can just use the power set if you want.

39 00:04:21,071 –> 00:04:26,529 The real question is therefore to find the most efficient sigma algebra.

40 00:04:26,660 –> 00:04:32,200 So where you have to add the least amount of sets to get to a sigma algebra

41 00:04:32,600 –> 00:04:35,557 and this is indeed the sigma M.

42 00:04:35,714 –> 00:04:39,614 To get used to this definition, let’s look at an easy example.

43 00:04:40,071 –> 00:04:47,214 Let’s look at a set with 4 elements. So let’s call them a, b, c and d

44 00:04:49,186 –> 00:04:55,386 and then we define a set of subsets. So maybe I just choose singletons.

45 00:04:55,387 –> 00:05:01,486 So this is just the subset that contains only a and this is just a subset that contains only b

46 00:05:01,900 –> 00:05:06,071 and I form the whole set. So this is my family of subsets.

47 00:05:06,914 –> 00:05:10,329 First thing to note, this is not a sigma algebra yet.

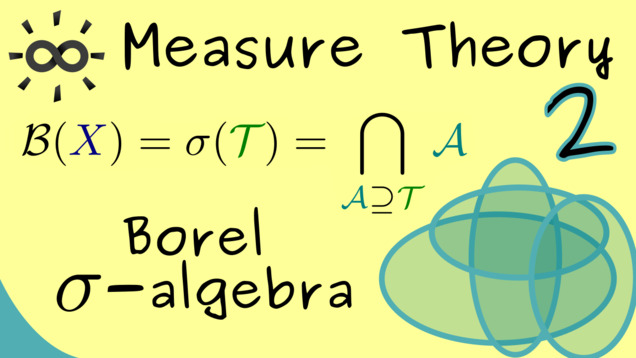
48 00:05:10,414 –> 00:05:19,214 So we can form now our sigma(M). Which should be the smallest sigma algebra that contains this family of subsets.

49 00:05:19,486 –> 00:05:23,943 We immediately know 2 things. First of all we know that it’s a sigma algebra.

50 00:05:23,986 –> 00:05:29,357 So we know it contains the empty set and the whole set X.

51 00:05:30,029 –> 00:05:33,314 This is the first property of the sigma algebra.

52 00:05:34,100 –> 00:05:39,100 The next thing we know is that it’s the sigma algebra that contains our set M.

53 00:05:39,215 –> 00:05:48,471 So therefore also “a” as a set and b as a set, has to be inside sigma(M).

54 00:05:48,729 –> 00:05:51,914 Now, if you thing about the other properties of the sigma algebra,

55 00:05:52,086 –> 00:05:59,157 we remember, that we know that all the countable unions are inside the sigma algebra.

56 00:05:59,300 –> 00:06:08,557 Countable unions is of course, union of these two sets. So we know that also {a,b} has to be inside the sigma algebra.

57 00:06:09,429 –> 00:06:18,114 All other unions we can form with these 4 sets don’t change anything. We still get out our X, the empty set or {a} or {b}.

58 00:06:18,115 –> 00:06:22,729 So these are all the unions we can form out of these 4 sets.

59 00:06:23,429 –> 00:06:30,771 Then let’s go to the one remaining property of a sigma algebra, namely that all the complements are also inside the sigma algebra.

60 00:06:31,300 –> 00:06:36,986 Which means here, the complement of {a} is of course {b,c,d}.

61 00:06:37,114 –> 00:06:44,414 There is also b inside the sigma algebra and the complement of b is of course {a,c,d}

62 00:06:45,043 –> 00:06:51,629 and then we also have to add the complement of {a,b}, which is {c,d}.

63 00:06:51,829 –> 00:06:58,229 Every step with did up to this point, were things we needed to do to reach a sigma algebra.

64 00:06:58,329 –> 00:07:02,300 So there was no other choice then adding all these elements here.

65 00:07:02,729 –> 00:07:08,771 The question still remains. Was this sufficient? So did we get to a sigma algebra yet?

66 00:07:09,214 –> 00:07:16,671 This is what we can now immediately check. So for example the first rule is fulfilled. Empty set are inside.

67 00:07:16,743 –> 00:07:23,214 All complements are inside. So if we look at complements here and here, we still see that all are there.

68 00:07:23,300 –> 00:07:31,443 Ok, then what about the unions? So we know the unions here and here fit together, but what about the unions here?

69 00:07:31,486 –> 00:07:37,557 So just check all possible unions and then you see, all the sets are there,

70 00:07:37,558 –> 00:07:43,186 we need to be stable under the operations of union and complements.

71 00:07:43,271 –> 00:07:47,700 So this means, what we have here is indeed a sigma algebra.

72 00:07:49,300 –> 00:07:55,248 and by construction it was the smallest one possible to get from M to sigma algebra.

73 00:07:55,249 –> 00:07:57,843 So this is indeed sigma(M).

74 00:07:58,086 –> 00:08:06,786 So what you saw here was that it’s not so hard to get to the sigma algebra, if we start with a finite set.

75 00:08:06,857 –> 00:08:14,986 So if you have finitely many elements, we can do all the finitely many operations to end at our sigma algebra.

76 00:08:15,714 –> 00:08:20,500 Obviously this has to be much harder if we start with an infinite set,

77 00:08:20,657 –> 00:08:26,414 because then we have to do infinitely many steps until we reach the sigma algebra

78 00:08:27,229 –> 00:08:34,143 and this leads us now to the most important sigma algebra and I will define it here.

79 00:08:34,914 –> 00:08:40,100 This works if our set X is a topological space.

80 00:08:40,186 –> 00:08:48,357 If you don’t know what a topological space is, you can work in the same way if your X is a metric space.

81 00:08:48,829 –> 00:08:57,086 If you also don’t know what a metric space is, then you can choose X more concretely as R or R^n if you want.

82 00:08:57,229 –> 00:09:04,400 These things work all the same, because the only ingredient we need here is to know what open sets are.

83 00:09:04,543 –> 00:09:12,357 Now you might already know what we want to do. We want to have all these open sets in our sigma algebra.

84 00:09:13,071 –> 00:09:22,871 Which means we will look at a sigma algebra that the open sets generate and indeed, this is the Borel sigma algebra.

85 00:09:23,086 –> 00:09:25,629 Denoted by B(X).

86 00:09:26,343 –> 00:09:32,280 This is the sigma algebra generated by the open sets.

87 00:09:32,280 –> 00:09:36,043 If you are working in a topological space, normally you would say,

88 00:09:36,143 –> 00:09:44,243 Ok, I have my set X together with a topology. So this could be my T and call this a topological space

89 00:09:44,400 –> 00:09:48,057 and the topology are just the open sets.

90 00:09:48,171 –> 00:09:57,529 Which means by our definition from above, our Borel sigma algebra is nothing more than sigma of this topology.

91 00:09:59,371 –> 00:10:06,200 And this is the Borel sigma algebra. Maybe to be more concrete, it’s the Borel sigma algebra on X.

92 00:10:06,371 –> 00:10:11,586 What you should note is that in our notation, the topology vanishes.

93 00:10:11,643 –> 00:10:20,009 So there is no mention of this topology inside B(X), because most of the time the topology is clear.

94 00:10:20,729 –> 00:10:24,686 It’s also obvious which topology or metric we use.

95 00:10:25,043 –> 00:10:32,429 For example, in R^n we use our standard topology, so we know what the open sets in R^n are

96 00:10:32,514 –> 00:10:37,957 and therefore we immediately know what the Borel sigma algebra of R^n is.

97 00:10:38,400 –> 00:10:43,157 Therefore you really should keep in mind that by definition of the Borel sigma algebra,

98 00:10:43,171 –> 00:10:50,471 it includes the topological structure, so what open means, into a sigma algebra

99 00:10:50,629 –> 00:10:57,149 and in the case of R^n, this is indeed a really big sigma algebra, but not a power set.

100 00:10:57,150 –> 00:11:04,500 So it’s not the biggest possible sigma algebra, but it’s the most suitable sigma algebra in our context,

101 00:11:05,057 –> 00:11:11,429 because it contains all the sets we want to measure and this is what we will do in the next video,

102 00:11:11,486 –> 00:11:14,500 where I want to define what a measure is

103 00:11:14,714 –> 00:11:24,286 and there you will see that in the case of R^n, we need this Borel sigma algebra and can’t choose the power set,

104 00:11:24,287 –> 00:11:28,286 because our measure should fulfill some meaningful rules.

105 00:11:28,871 –> 00:11:34,714 And these rules can’t be fulfilled on the whole power set, but on the Borel sigma algebra

106 00:11:34,986 –> 00:11:39,443 and the Borel sigma algebra is big enough. There are a lot of sets inside.

107 00:11:39,600 –> 00:11:42,714 Indeed all the sets are inside, we want to measure in the end.

108 00:11:43,443 –> 00:11:46,957 Then thank you very much and see you next time.

Q1: An element in a $\sigma$-algebra is called a measurable set.

A1: True

A2: False

Q2: For a set $A \subseteq X$, we can generally calculate the generated $\sigma$-algebra.

A1: $\sigma({A}) = { A }$

A2: $\sigma({A}) = { \emptyset, A, A^c, X }$

A3: $\sigma({A}) = { \emptyset, A, X }$

Q3: The Borel $\sigma$-algebra is generated by the open sets. Which of the statements is false?

A1: $[0,1] \in \mathcal{B}(\mathbb{R})$

A2: $(0,1) \cup [2,4] \in \mathcal{B}(\mathbb{R})$

A3: $\mathbb{N} \notin \mathcal{B}(\mathbb{R})$

A4: $\emptyset \in \mathcal{B}(\mathbb{R})$

Q4: Is the Borel $\sigma$-algebra $\mathcal{B}(\mathbb{R})$ equal to the power set of $\mathbb{R}$?

A1: Yes, it is.

A2: No, it isn’t.