-
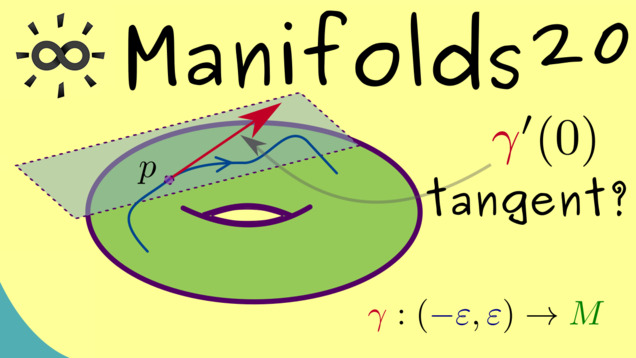
Title: Tangent Curves
-
Series: Manifolds
-
YouTube-Title: Manifolds 20 | Tangent Curves
-
Bright video: https://youtu.be/6ULTQ7nfItw
-
Dark video: https://youtu.be/fClddpoMvP8
-
Ad-free video: Watch Vimeo video
-
Quiz: Test your knowledge
-
Dark-PDF: Download PDF version of the dark video
-
Print-PDF: Download printable PDF version
-
Thumbnail (bright): Download PNG
-
Thumbnail (dark): Download PNG
-
Subtitle on GitHub: mf20_sub_eng.srt missing
-
Timestamps (n/a)
-
Subtitle in English (n/a)
-
Quiz Content
Q1: How can the tangent space for a submanifold be described?
A1: $$ T^{\mathrm{sub}}_p(M) = { \gamma^\prime(0) \mid \gamma: (-\varepsilon, \varepsilon) \rightarrow M , , \gamma(0) = p } $$
A2: $$ T^{\mathrm{sub}}_p(M) = { \gamma(0) \mid \gamma: (-\varepsilon, \varepsilon) \rightarrow M \text{ with } \gamma(1) = 0 } $$
A3: $$ T^{\mathrm{sub}}_p(M) = { \gamma(0) \mid \gamma: (-\varepsilon, \varepsilon) \rightarrow M } $$
A4: $$ T^{\mathrm{sub}}_p(M) = { \gamma^\prime(0) \mid \gamma: (-\varepsilon, \varepsilon) \rightarrow M } $$
-
Last update: 2024-10