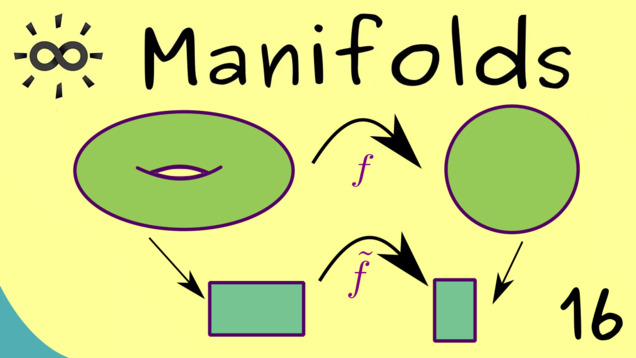
-
Title: Smooth Maps (Definition)
-
Series: Manifolds
-
Bright video: https://youtu.be/6tDVa5XVW2E
-
Dark video: https://youtu.be/tfbQprmtGVE
-
Quiz: Test your knowledge
-
Print-PDF: Download printable PDF version
-
Thumbnail (bright): Download PNG
-
Timestamps
-
Subtitle in English
