-
Title: Inner Products and Hilbert Spaces
-
Series: Functional Analysis
-
YouTube-Title: Functional Analysis 8 | Inner Products and Hilbert Spaces
-
Bright video: https://youtu.be/UzSEvb9AJYw
-
Dark video: https://youtu.be/VxgoXvo84fE
-
Ad-free video: Watch Vimeo video
-
Quiz: Test your knowledge
-
Dark-PDF: Download PDF version of the dark video
-
Print-PDF: Download printable PDF version
-
Thumbnail (bright): Download PNG
-
Thumbnail (dark): Download PNG
-
Subtitle on GitHub: fa08_sub_eng.srt
-
Timestamps
00:00 Introduction
02:25 Inner product definition
06:25 Norm and Hilbert space
-
Subtitle in English
1 00:00:00,469 –> 00:00:02,210 Hello and welcome back to
2 00:00:02,220 –> 00:00:03,390 functional analysis.
3 00:00:03,500 –> 00:00:04,610 And as always, I want to
4 00:00:04,619 –> 00:00:06,090 thank all the nice people
5 00:00:06,099 –> 00:00:07,780 that support my channel on
6 00:00:07,789 –> 00:00:08,920 Steady or PayPal.
7 00:00:09,739 –> 00:00:11,229 In today’s part eight, we
8 00:00:11,239 –> 00:00:12,819 introduce inner products
9 00:00:12,829 –> 00:00:14,130 and Hilbert spaces.
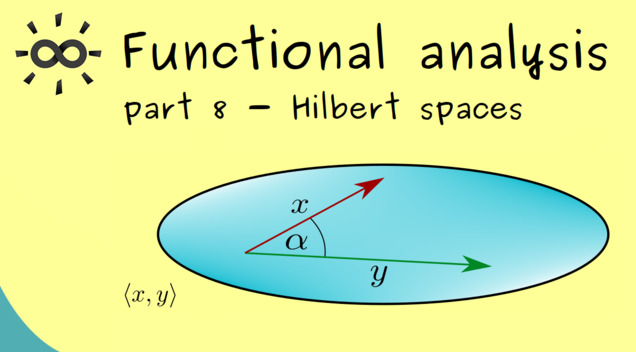
10 00:00:15,250 –> 00:00:16,819 You will see such an inner
11 00:00:16,829 –> 00:00:18,399 product gives the space more
12 00:00:18,409 –> 00:00:19,149 structure.
13 00:00:19,309 –> 00:00:20,950 So maybe let’s recall which
14 00:00:20,959 –> 00:00:22,309 structures we already know.
15 00:00:22,840 –> 00:00:24,040 First, we discussed
16 00:00:24,049 –> 00:00:25,870 metrics and we learned
17 00:00:25,879 –> 00:00:27,270 that a metric measures
18 00:00:27,280 –> 00:00:28,700 distances in the space.
19 00:00:29,739 –> 00:00:31,280 Afterwards, we introduced
20 00:00:31,290 –> 00:00:33,240 norms for vector spaces
21 00:00:34,029 –> 00:00:35,229 and there we learned that
22 00:00:35,240 –> 00:00:36,569 a norm measures distances
23 00:00:36,580 –> 00:00:38,250 as well, but it also
24 00:00:38,259 –> 00:00:39,750 measures lengths of
25 00:00:39,759 –> 00:00:40,369 vectors.
26 00:00:41,099 –> 00:00:42,669 And now an inner product
27 00:00:42,680 –> 00:00:43,990 should do even more in a
28 00:00:44,000 –> 00:00:44,869 vector space.
29 00:00:45,549 –> 00:00:47,270 Besides measuring distances
30 00:00:47,279 –> 00:00:49,209 and lengths, it is also able
31 00:00:49,220 –> 00:00:51,119 to measure angles between
32 00:00:51,130 –> 00:00:51,880 two vectors.
33 00:00:52,580 –> 00:00:54,119 So you see an inner product
34 00:00:54,130 –> 00:00:56,020 gives you a geometry like
35 00:00:56,029 –> 00:00:57,279 you naturally have it on
36 00:00:57,290 –> 00:00:58,599 the plane or the surrounding
37 00:00:58,610 –> 00:00:59,080 space.
38 00:00:59,779 –> 00:01:01,349 The usual notation one uses
39 00:01:01,360 –> 00:01:03,009 for an inner product is given
40 00:01:03,020 –> 00:01:04,319 by these brackets.
41 00:01:05,080 –> 00:01:06,779 So what we have is one vector
42 00:01:06,790 –> 00:01:08,349 x on the left-hand side and
43 00:01:08,360 –> 00:01:09,970 another vector y on the right-
44 00:01:09,980 –> 00:01:11,809 hand side. A nice
45 00:01:11,819 –> 00:01:13,290 visualization for this would
46 00:01:13,300 –> 00:01:15,169 be to have the vector x on
47 00:01:15,180 –> 00:01:16,360 the horizontal line
48 00:01:17,169 –> 00:01:18,930 and the vector y in another
49 00:01:18,940 –> 00:01:20,349 direction as an arrow,
50 00:01:21,099 –> 00:01:22,849 which means in this picture,
51 00:01:22,860 –> 00:01:24,610 we find an angle which we
52 00:01:24,620 –> 00:01:25,599 could call alpha
53 00:01:25,610 –> 00:01:26,330 for example.
54 00:01:27,120 –> 00:01:28,629 Now the inner product should
55 00:01:28,639 –> 00:01:30,160 be a multiplication of these
56 00:01:30,169 –> 00:01:31,889 two vectors where only the
57 00:01:31,900 –> 00:01:33,279 component of y
58 00:01:33,300 –> 00:01:34,889 in the direction of x is
59 00:01:34,900 –> 00:01:36,459 needed. In the
60 00:01:36,470 –> 00:01:37,050 picture
61 00:01:37,059 –> 00:01:38,400 this would mean that we have
62 00:01:38,410 –> 00:01:40,099 here a wide angle and
63 00:01:40,110 –> 00:01:41,900 only look at this arrow here.
64 00:01:42,470 –> 00:01:43,709 Now, since you’re good with
65 00:01:43,720 –> 00:01:45,059 trigonometric functions,
66 00:01:45,069 –> 00:01:46,419 you can easily calculate
67 00:01:46,430 –> 00:01:48,059 the length of this yellow
68 00:01:48,069 –> 00:01:48,580 arrow.
69 00:01:49,230 –> 00:01:50,889 It is simply the length of
70 00:01:50,900 –> 00:01:52,389 y times the
71 00:01:52,800 –> 00:01:53,900 cosine of alpha.
72 00:01:54,949 –> 00:01:56,430 And this length now should
73 00:01:56,440 –> 00:01:58,209 be multiplied with the length
74 00:01:58,220 –> 00:01:59,519 of the arrow x
75 00:02:00,389 –> 00:02:02,209 and this formula now explains
76 00:02:02,220 –> 00:02:03,529 what we want from an inner
77 00:02:03,540 –> 00:02:04,169 product.
78 00:02:04,760 –> 00:02:06,089 However, it does not define
79 00:02:06,099 –> 00:02:06,769 anything yet.
80 00:02:06,779 –> 00:02:07,910 It does not explain what
81 00:02:07,919 –> 00:02:09,258 a norm should mean here
82 00:02:09,369 –> 00:02:10,820 and what the angle alpha
83 00:02:10,830 –> 00:02:12,369 is in a general vector space.
84 00:02:13,169 –> 00:02:14,360 Of course, the correct logic
85 00:02:14,369 –> 00:02:15,759 should be that we start with
86 00:02:15,770 –> 00:02:17,110 an inner product, then we
87 00:02:17,119 –> 00:02:18,630 define norm and then we
88 00:02:18,639 –> 00:02:20,429 define the angle such that
89 00:02:20,440 –> 00:02:21,759 we get a formula in this
90 00:02:21,770 –> 00:02:22,149 sense.
91 00:02:23,179 –> 00:02:24,490 In order to do that, we now
92 00:02:24,500 –> 00:02:26,289 finally state the definition.
93 00:02:27,240 –> 00:02:28,720 As usual, we use the letter
94 00:02:28,729 –> 00:02:30,539 F to denote either R or
95 00:02:30,550 –> 00:02:32,490 C and then X
96 00:02:32,500 –> 00:02:34,199 should be just an F-vector
97 00:02:34,210 –> 00:02:34,660 space.
98 00:02:35,679 –> 00:02:36,979 Now, the inner product is
99 00:02:36,990 –> 00:02:38,979 just a map where we use these
100 00:02:38,990 –> 00:02:39,839 angle brackets
101 00:02:39,850 –> 00:02:41,520 again. The
102 00:02:41,529 –> 00:02:43,389 input is two vectors, such
103 00:02:43,399 –> 00:02:44,639 that the domain should be
104 00:02:44,649 –> 00:02:46,029 X times X.
105 00:02:46,750 –> 00:02:48,199 We’ve already discussed that
106 00:02:48,210 –> 00:02:49,619 the outcome should be just
107 00:02:49,630 –> 00:02:50,259 a number.
108 00:02:50,270 –> 00:02:51,850 So a scalar in F
109 00:02:52,500 –> 00:02:53,970 and there we already see
110 00:02:53,979 –> 00:02:55,809 that if we are in the complex
111 00:02:55,820 –> 00:02:57,309 numbers, in a complex vector
112 00:02:57,320 –> 00:02:58,699 space, this formula from
113 00:02:58,710 –> 00:03:00,130 above can’t be completely
114 00:03:00,139 –> 00:03:00,529 true.
115 00:03:01,520 –> 00:03:02,850 So let’s use some quotation
116 00:03:02,860 –> 00:03:04,619 marks to say that this was
117 00:03:04,630 –> 00:03:06,449 just an informal explanation
118 00:03:06,460 –> 00:03:07,240 at the beginning.
119 00:03:07,750 –> 00:03:09,229 Nevertheless, it can still
120 00:03:09,240 –> 00:03:10,789 guide us through the definition
121 00:03:10,800 –> 00:03:11,110 here.
122 00:03:11,850 –> 00:03:12,220 OK.
123 00:03:12,229 –> 00:03:13,589 Now, such a map is called
124 00:03:13,600 –> 00:03:14,380 an inner product,
125 00:03:14,389 –> 00:03:16,360 if it fulfills three properties.
126 00:03:16,919 –> 00:03:18,110 The first property tells
127 00:03:18,119 –> 00:03:19,250 us that the inner product
128 00:03:19,259 –> 00:03:20,600 should be able to measure
129 00:03:20,610 –> 00:03:21,139 lengths.
130 00:03:21,979 –> 00:03:23,770 This means that if we put
131 00:03:23,779 –> 00:03:25,729 the same vector x into both
132 00:03:25,740 –> 00:03:27,289 sides, then the
133 00:03:27,300 –> 00:03:28,539 outcome should be a non-negative
134 00:03:29,300 –> 00:03:30,970 real number. No matter if
135 00:03:30,979 –> 00:03:31,949 we are in the real or the
136 00:03:31,960 –> 00:03:32,809 complex case.
137 00:03:33,639 –> 00:03:35,169 On the other hand, you already
138 00:03:35,179 –> 00:03:36,970 know length zero should be
139 00:03:36,979 –> 00:03:38,660 only possible for the zero
140 00:03:38,669 –> 00:03:39,199 vector.
141 00:03:40,050 –> 00:03:41,779 In other words, <x,x> is
142 00:03:41,789 –> 00:03:43,720 zero if and only if
143 00:03:43,729 –> 00:03:45,100 x is the zero vector.
144 00:03:45,830 –> 00:03:47,110 Of course, you recognize
145 00:03:47,119 –> 00:03:48,820 this property, it’s called
146 00:03:48,830 –> 00:03:50,059 positive definite.
147 00:03:50,710 –> 00:03:51,779 Indeed, you see it’s the
148 00:03:51,789 –> 00:03:53,460 same first property as we
149 00:03:53,470 –> 00:03:54,490 had it for the norm.
150 00:03:55,320 –> 00:03:56,630 Now, the second property
151 00:03:56,639 –> 00:03:58,350 is about what changes when
152 00:03:58,360 –> 00:04:00,009 we exchange the two vectors
153 00:04:00,020 –> 00:04:01,020 in the inner product.
154 00:04:01,929 –> 00:04:03,130 Having a picture from above
155 00:04:03,139 –> 00:04:04,830 in mind, you see we still
156 00:04:04,839 –> 00:04:05,960 have the same angle.
157 00:04:05,970 –> 00:04:06,940 So it shouldn’t make any
158 00:04:06,949 –> 00:04:08,270 difference when we exchange
159 00:04:08,279 –> 00:04:09,039 the two vectors.
160 00:04:10,160 –> 00:04:11,539 So this should be
161 00:04:11,820 –> 00:04:13,380 <y,x>.
162 00:04:14,649 –> 00:04:16,178 However, this only makes
163 00:04:16,190 –> 00:04:17,709 sense in the case that we
164 00:04:17,720 –> 00:04:19,399 are in a real vector space.
165 00:04:19,410 –> 00:04:21,200 So our F is indeed
166 00:04:21,209 –> 00:04:21,678 R.
167 00:04:22,859 –> 00:04:24,600 Now from complex vector space,
168 00:04:24,609 –> 00:04:26,279 we’ve already seen that this
169 00:04:26,290 –> 00:04:27,799 equation here can’t be the
170 00:04:27,809 –> 00:04:28,739 complete truth.
171 00:04:29,429 –> 00:04:31,230 Indeed, the complex conjugation
172 00:04:31,239 –> 00:04:32,600 has to be involved here.
173 00:04:33,329 –> 00:04:34,589 Please keep in mind that
174 00:04:34,600 –> 00:04:36,230 in the first property also,
175 00:04:36,239 –> 00:04:37,970 in a complex case, we want
176 00:04:37,980 –> 00:04:39,709 to get out a real number,
177 00:04:39,720 –> 00:04:41,029 when we put in the same vector
178 00:04:41,040 –> 00:04:41,540 twice.
179 00:04:42,420 –> 00:04:43,929 So therefore, if we exchange
180 00:04:43,940 –> 00:04:45,640 these two vector here, we also
181 00:04:45,649 –> 00:04:47,609 have to add a complex conjugation.
182 00:04:48,559 –> 00:04:49,959 For this reason, we call
183 00:04:49,970 –> 00:04:51,459 this property conjugate
184 00:04:51,470 –> 00:04:52,779 symmetry or just
185 00:04:52,790 –> 00:04:54,450 symmetry, if we are in a real
186 00:04:54,459 –> 00:04:54,899 case.
187 00:04:55,559 –> 00:04:56,989 And now the third and last
188 00:04:57,000 –> 00:04:58,970 property should finally be
189 00:04:58,980 –> 00:04:59,899 the linearity.
190 00:05:00,700 –> 00:05:02,089 The linearity makes sense,
191 00:05:02,100 –> 00:05:03,070 if you look at the picture
192 00:05:03,079 –> 00:05:04,720 again. If you scale
193 00:05:04,730 –> 00:05:06,230 y or if you add another
194 00:05:06,239 –> 00:05:08,209 vector, then you could just
195 00:05:08,220 –> 00:05:09,790 do the same with the outcome.
196 00:05:10,690 –> 00:05:11,910 For the formula, we then
197 00:05:11,920 –> 00:05:13,049 need two vectors.
198 00:05:13,059 –> 00:05:14,640 So let’s call them y_1
199 00:05:14,649 –> 00:05:16,309 and y_2 and add them.
200 00:05:17,589 –> 00:05:18,529 The inner product should
201 00:05:18,540 –> 00:05:19,670 be additive in the second
202 00:05:19,679 –> 00:05:21,089 component, which means we
203 00:05:21,100 –> 00:05:22,570 can pull out the addition
204 00:05:22,579 –> 00:05:22,890 here.
205 00:05:23,339 –> 00:05:24,429 Of course, it should also
206 00:05:24,440 –> 00:05:26,109 be homogeneous, which means
207 00:05:26,119 –> 00:05:27,600 we can pull out a scalar.
208 00:05:28,299 –> 00:05:29,720 So let’s call that scalar
209 00:05:29,730 –> 00:05:30,359 lambda.
210 00:05:30,369 –> 00:05:31,549 And then the equation looks
211 00:05:31,559 –> 00:05:33,510 like this, which means
212 00:05:33,519 –> 00:05:34,769 that on the right-hand side,
213 00:05:34,779 –> 00:05:36,459 we just have the multiplication
214 00:05:36,470 –> 00:05:38,070 of two numbers in F.
215 00:05:38,820 –> 00:05:40,190 And indeed, that’s the part
216 00:05:40,200 –> 00:05:41,640 that only works in the second
217 00:05:41,649 –> 00:05:43,269 component, because if you
218 00:05:43,279 –> 00:05:44,640 want to do that in the first
219 00:05:44,649 –> 00:05:46,269 component as well, you have
220 00:05:46,279 –> 00:05:47,600 to use property two.
221 00:05:48,299 –> 00:05:49,619 And that one tells you, you
222 00:05:49,630 –> 00:05:50,799 don’t have any problem in
223 00:05:50,809 –> 00:05:51,670 the real case,
224 00:05:51,679 –> 00:05:53,239 but in the complex case,
225 00:05:53,250 –> 00:05:55,109 you get out lambda bar
226 00:05:55,119 –> 00:05:55,920 instead of lambda.
227 00:05:56,690 –> 00:05:58,079 So please keep that in mind.
228 00:05:58,089 –> 00:05:59,880 Both sides are not the same.
229 00:06:00,709 –> 00:06:02,059 And here we have chosen the
230 00:06:02,070 –> 00:06:03,700 second part to be the linear
231 00:06:03,709 –> 00:06:04,059 one.
232 00:06:04,700 –> 00:06:06,399 I emphasize that because
233 00:06:06,410 –> 00:06:07,950 there are other people that
234 00:06:07,959 –> 00:06:09,359 choose the first part to
235 00:06:09,369 –> 00:06:10,339 be the linear one.
236 00:06:10,890 –> 00:06:12,440 Therefore, please be careful
237 00:06:12,450 –> 00:06:12,720 there.
238 00:06:13,570 –> 00:06:14,000 OK.
239 00:06:14,010 –> 00:06:15,670 So that’s the whole definition
240 00:06:15,679 –> 00:06:16,829 of an inner product
241 00:06:16,950 –> 00:06:18,350 and the vector space X
242 00:06:18,359 –> 00:06:20,059 together with an inner product,
243 00:06:20,070 –> 00:06:21,940 we just call an inner product
244 00:06:21,950 –> 00:06:22,309 space.
245 00:06:23,149 –> 00:06:24,609 Now, an important part we’ve
246 00:06:24,619 –> 00:06:26,269 already mentioned is that
247 00:06:26,279 –> 00:06:27,730 in an inner product space,
248 00:06:27,739 –> 00:06:29,279 we can measure lengths
249 00:06:29,799 –> 00:06:31,329 and we can do that simply
250 00:06:31,339 –> 00:06:32,929 by defining a norm.
251 00:06:32,940 –> 00:06:34,850 And we do this by using the
252 00:06:34,859 –> 00:06:36,010 formula from above.
253 00:06:36,019 –> 00:06:37,989 So we set the norm of x
254 00:06:38,000 –> 00:06:39,320 to be the square root of
255 00:06:39,329 –> 00:06:40,209 the inner product
256 00:06:41,100 –> 00:06:43,079 by using these three properties.
257 00:06:43,089 –> 00:06:44,929 It’s indeed easy to show
258 00:06:44,940 –> 00:06:46,559 that this defines a norm
259 00:06:47,250 –> 00:06:48,910 and if we need to be careful
260 00:06:48,920 –> 00:06:50,420 which norm we talk about,
261 00:06:50,450 –> 00:06:52,429 we can set the inner product
262 00:06:52,440 –> 00:06:53,510 as an index here.
263 00:06:54,350 –> 00:06:55,809 Now, to close this video,
264 00:06:55,820 –> 00:06:57,540 I’ll tell you now what a Hilbert
265 00:06:57,549 –> 00:06:59,399 space is. An
266 00:06:59,410 –> 00:07:00,799 inner product space, which
267 00:07:00,809 –> 00:07:02,500 means X together with an
268 00:07:02,510 –> 00:07:04,489 inner product, is
269 00:07:04,500 –> 00:07:06,209 called a Hilbert space,
270 00:07:07,260 –> 00:07:08,730 if X together with the
271 00:07:08,739 –> 00:07:10,619 corresponding norm is a banach
272 00:07:10,630 –> 00:07:11,380 space.
273 00:07:12,040 –> 00:07:13,920 So this means we have a vector
274 00:07:13,929 –> 00:07:15,339 space, where we can measure
275 00:07:15,350 –> 00:07:16,950 lengths and angles and it’s
276 00:07:16,959 –> 00:07:18,739 also a complete metric space.
277 00:07:19,779 –> 00:07:20,239 OK,
278 00:07:20,250 –> 00:07:21,149 I think that’s good enough
279 00:07:21,160 –> 00:07:21,859 for today.
280 00:07:21,869 –> 00:07:23,660 I see you next time when
281 00:07:23,670 –> 00:07:25,250 we discuss examples of Hilbert
282 00:07:25,260 –> 00:07:25,829 spaces.
283 00:07:26,540 –> 00:07:28,119 So have a nice day and see
284 00:07:28,130 –> 00:07:28,640 you then.
285 00:07:28,649 –> 00:07:29,279 Bye.
-
Quiz Content
Q1: Let $\langle \cdot, \cdot \rangle$ be an inner product on $\mathbb{C}^n$. What is not correct in general?
A1: $\langle x, y \rangle = 0$ implies $x = y$
A2: $\langle x, x \rangle = 0$ implies $x = 0$
A3: $\langle x, 0 \rangle = 0$ for all $x \in \mathbb{C}^n$
A4: $\langle x, i y\rangle = - \langle i x, y\rangle$ for all $x,y \in \mathbb{C}^n$
Q2: Is $\mathbb{R}^n$ together with the standard inner product a Hilbert space?
A1: Yes!
A2: No!
A3: One needs more information.
Q3: Is $\mathbb{C}^n$ together with the standard inner product a Hilbert space?
A1: Yes!
A2: No!
A3: One needs more information.
-
Last update: 2024-10