-
Title: Norms and Banach Spaces
-
Series: Functional Analysis
-
YouTube-Title: Functional Analysis 6 | Norms and Banach Spaces
-
Bright video: https://youtu.be/imYQJOgUx7Y
-
Dark video: https://youtu.be/Slmtlv3g0C8
-
Ad-free video: Watch Vimeo video
-
Quiz: Test your knowledge
-
Dark-PDF: Download PDF version of the dark video
-
Print-PDF: Download printable PDF version
-
Exercise Download PDF sheets
-
Thumbnail (bright): Download PNG
-
Thumbnail (dark): Download PNG
-
Subtitle on GitHub: fa06_sub_eng.srt
-
Timestamps
00:00 Introduction
00:33 Definition (norm)
04:17 Normed space
04:50 Connection to metrics
06:00 Banach space
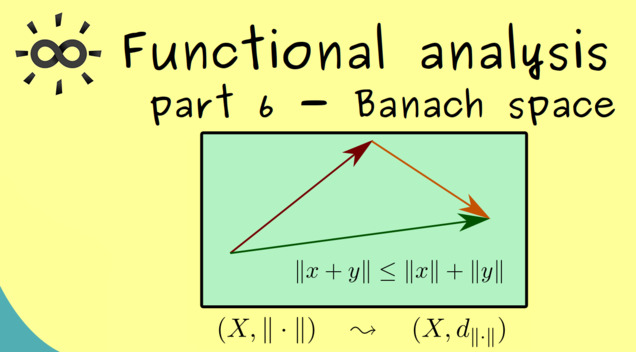
-
Subtitle in English
1 00:00:00,420 –> 00:00:06,780 hello and welcome back to functional analysis and as always I want to thank all the nice people that
2 00:00:06,780 –> 00:00:14,760 support the channel on Steady or PayPal today’s part 6 finally is about Banach spaces. We will
3 00:00:14,760 –> 00:00:20,340 later see that a so-called Banach space is indeed one of the most important objects in functional
4 00:00:20,340 –> 00:00:28,140 analysis. In its core it’s just a vector space but with more analytical structure on it. In order to
5 00:00:28,140 –> 00:00:34,980 understand such a Banach space we first have to define what a norm is. For this, I will use the
6 00:00:34,980 –> 00:00:42,420 letter F to denote a field of numbers. However here it will always be the real or the complex numbers.
7 00:00:43,500 –> 00:00:48,660 Of course, this makes our life easier because we don’t have to write down the definition two times.
8 00:00:49,740 –> 00:00:55,800 Now we have a set X that also carries some operations such that it is a vector space.
9 00:00:57,000 –> 00:01:04,140 F Vector space always means that the scaling of vectors is done with numbers form F. This
10 00:01:04,140 –> 00:01:10,800 means if F is R you can scale with real numbers and in the case that F is C you can scale even
11 00:01:10,800 –> 00:01:19,320 with complex numbers. The usual visualization for points in a vector space is given by arrows. It’s
12 00:01:19,320 –> 00:01:24,720 a good idea because you see the two operations scaling and adding two vectors immediately.
13 00:01:25,560 –> 00:01:31,680 However from the analytical point of view it would be also nice to know how long such an arrow is.
14 00:01:32,520 –> 00:01:36,660 Measuring such a length is what we call in the abstract sense and norm.
15 00:01:37,500 –> 00:01:43,140 The symbol one uses for a norm are just two lines on the left and two lines on the right.
16 00:01:43,980 –> 00:01:49,380 And because we are measuring a length, the only possible values should be non-negative numbers.
17 00:01:50,340 –> 00:01:56,160 This means that each Vector in X gets a number which is positive or zero,
18 00:01:56,160 –> 00:02:00,840 and this map we get we call a norm if it fulfills three properties.
19 00:02:01,920 –> 00:02:06,540 Since you already know metrics you might easily guess some of the details here.
20 00:02:07,500 –> 00:02:13,920 For example in (a) we find the positive definite part which means if we have the length 0,
21 00:02:15,480 –> 00:02:21,240 then this is equivalent for having the zero vector, or in other words the zero
22 00:02:21,240 –> 00:02:26,400 vector has length 0 (which makes sense) but it’s also the only one with length 0.
23 00:02:27,000 –> 00:02:34,140 Now Part (b) explains what happens to the length when we scale a vector. Scaling here means we
24 00:02:34,140 –> 00:02:41,760 have a vector x and multiply it from the left with a scalar so a number in F. In the
25 00:02:41,760 –> 00:02:47,460 picture you always visualize that with the arrow getting longer or smaller depending on Lambda.
26 00:02:48,540 –> 00:02:55,800 Hence the norm has to satisfy this which means the length gets also multiplied by this Factor Lambda.
27 00:02:57,480 –> 00:03:03,240 However Lambda could be a negative number or even a complex one such that this only makes
28 00:03:03,240 –> 00:03:10,380 sense if we consider the absolute value of Lambda. Now depending what F is, R or C, we have here the
29 00:03:10,380 –> 00:03:15,900 absolute value in the real numbers or in the complex numbers. Therefore this part (b) now tells
30 00:03:15,900 –> 00:03:23,100 you that the norm is always absolutely homogeneous. So you can always pull out scalars but outside of
31 00:03:23,100 –> 00:03:29,520 the norm they always get absolute values. Okay so we are in a vector space we have two operations
32 00:03:29,520 –> 00:03:34,920 the scalar multiplication we had in (b) and now in (c) we have to explain what happens under the addition.
33 00:03:35,700 –> 00:03:41,880 So let’s look at two vectors x and y. You already know how to visualize
34 00:03:41,880 –> 00:03:46,980 the addition in a vector space: you just put the two arrows together to get out the sum.
35 00:03:48,000 –> 00:03:53,820 Then you see the triangle here and you think that the length the norm should fulfill the
36 00:03:53,820 –> 00:04:00,420 normal geometry in this sense this means that it satisfies the triangle inequality.
37 00:04:01,860 –> 00:04:06,960 It looks similar what we have for the metrics but keep in mind here’s with respect to the vector
38 00:04:06,960 –> 00:04:14,160 addition. Therefore the norm is not a linear map in general because you can pull out the addition but
39 00:04:14,160 –> 00:04:20,820 what you get is only an inequality. Now you might already guess that a vector space together with a
40 00:04:20,820 –> 00:04:27,600 chosen norm gets a special name and you are right. This pair is what we simply call a normed space.
41 00:04:28,680 –> 00:04:34,560 So what we have is a real or complex vector space where we can measure the length in a meaningful
42 00:04:34,560 –> 00:04:41,040 way. Now you might ask what is the connection to the metric spaces we defined at the beginning s 43 00:04:41,040 –> 00:04:47,460 of this video series. Since the property (a) and (c) look very similar, the norm could be
44 00:04:47,460 –> 00:04:52,860 a special case of a metric. Indeed this one is an important fact you always should remember.
45 00:04:53,940 –> 00:05:01,020 If you have a norm for the vector space X, you can immediately define a metric. So maybe let’s put the
46 00:05:01,020 –> 00:05:06,960 norm in the index of the metric and then we can define the distance between two points x and y.
47 00:05:07,860 –> 00:05:13,740 If we look at the elements of the set X, we should think of the end points of the arrows,
48 00:05:14,640 –> 00:05:19,620 and then the distance between the two points should be given by the connection vector which
49 00:05:19,620 –> 00:05:28,140 is x minus y and then we take the length of it. In fact, this then defines a metric for the set X.
50 00:05:29,220 –> 00:05:32,640 This one is not hard to show. I advise you to try it out.
51 00:05:33,300 –> 00:05:38,460 So proving the three properties of the metric by just using the three properties of the norm.
52 00:05:39,660 –> 00:05:45,780 Now the most important thing to remember here is because we always have this definition in mind and
53 00:05:45,780 –> 00:05:52,200 a normed space is indeed a special case of a metric space. In particular all the definitions we have
54 00:05:52,200 –> 00:06:00,840 for metric spaces also work for normed spaces. So for example closedness, openness and so on. And with this
55 00:06:00,840 –> 00:06:06,900 in mind we can now eventually define what a Banach space is. So it could happen that our new
56 00:06:06,900 –> 00:06:15,000 metric space here (X,d) is a complete one. This one is a very nice property which we discussed in the
57 00:06:15,000 –> 00:06:23,460 last video. All the Cauchy sequences converge. We don’t have holes in this metric space. In this case
58 00:06:23,460 –> 00:06:31,620 then the original normed space, X with its norm, gets a special name: we call it a Banach space.
59 00:06:32,640 –> 00:06:38,580 Okay so now you know the definition of one of the most important objects in functional analysis.
60 00:06:39,300 –> 00:06:46,200 So you see we have ingredients from the algebraic side and also from the analytical side. On the one
61 00:06:46,200 –> 00:06:52,800 hand we have a real or complex vector space and on the other hand we have a complete metric space.
62 00:06:54,120 –> 00:06:58,740 And the thing that connects both sides very smoothly is our norm.
63 00:06:59,700 –> 00:07:04,620 So please keep that in mind we don’t have any metric here we have the metric that comes from
64 00:07:04,620 –> 00:07:11,700 this norm and by definition the norm can deal with the algebraic operations. So this
65 00:07:11,700 –> 00:07:18,480 is how I see a Banach space in the abstract sense to get more concrete we will look at a
66 00:07:18,480 –> 00:07:25,404 lot of examples in the next video so thanks for listening and I hope I see you there bye [Music]
-
Quiz Content
Q1: What is not a property of a norm?
A1: positive definite
A2: absolutely homogenous
A3: linear
A4: triangle inequality
Q2: Let $X = \mathbb{R}$ the vector space of real numbers. Is the absolute value $|\cdot|$ a norm on $X$?
A1: Yes!
A2: No!
Q3: What is the correct definition of a Banach space?
A1: A normed vector space that is also complex.
A2: A normed vector space that is also real.
A3: A normed vector space that is also complete.
A4: A normed vector space that is also a metric space.
-
Last update: 2024-10