-
Title: Exp, Cos and Sin as Power Series
-
Series: Complex Analysis
-
YouTube-Title: Complex Analysis 12 | Exp, Cos and Sin as Power Series
-
Bright video: Watch on YouTube
-
Dark video: Watch on YouTube
-
Ad-free video: Watch Vimeo video
-
Forum: Ask a question in Mattermost
-
Quiz: Test your knowledge
-
Dark-PDF: Download PDF version of the dark video
-
Print-PDF: Download printable PDF version
-
Thumbnail (bright): Download PNG
-
Thumbnail (dark): Download PNG
-
Subtitle on GitHub: ca12_sub_eng.srt
-
Download bright video: Link on Vimeo
-
Download dark video: Link on Vimeo
-
Timestamps
00:00 Intro
00:12 Derivatives of power series
01:28 Exponential function as a power series
03:28 Cosine as a power series
08:56 Sine as a power series
-
Subtitle in English
1 00:00:00,643 –> 00:00:03,838 Hello and welcome back to complex analysis
2 00:00:04,386 –> 00:00:11,327 and as you might know, first i want to thank all the nice people that support this channel on Steady, via Paypal or by other means.
3 00:00:11,943 –> 00:00:16,532 now in today’s part 12 we look at more examples for holomorphic functions.
4 00:00:17,529 –> 00:00:21,323 In particular we look at examples that are given by a power series,
5 00:00:22,314 –> 00:00:29,087 because we have already learned, a power series is a holomorphic function on its open disc of convergence.
6 00:00:29,514 –> 00:00:34,290 Also you know in the best case this disc is the whole complex plane.
7 00:00:35,171 –> 00:00:42,302 Now, please remind yourself, holomorphic just means that the complex derivative f’ exists everywhere.
8 00:00:43,114 –> 00:00:49,941 Moreover we also have shown that f’ is then also a power series with the same disc of convergence.
9 00:00:50,357 –> 00:00:55,158 In conclusion this means that f’ is also holomorphic.
10 00:00:56,114 –> 00:01:00,886 Hence the second derivative f’’ does also exist
11 00:01:01,200 –> 00:01:06,086 and by the same reasoning it’s also a power series with the same disc of convergence.
12 00:01:06,629 –> 00:01:12,018 So you see where this goes. All derivatives of f exist and are holomorphic functions.
13 00:01:13,214 –> 00:01:15,900 Ok, this is something you really should remember.
14 00:01:16,100 –> 00:01:20,914 It’s a strong result that holds for holomorphic functions that are given by a power series.
15 00:01:21,514 –> 00:01:27,538 Indeed later we will see that for all holomorphic functions the higher derivatives exist,
16 00:01:28,314 –> 00:01:31,449 but first let’s discuss some important examples.
17 00:01:32,586 –> 00:01:36,060 The first one, again should be the exponential function.
18 00:01:37,000 –> 00:01:43,350 Here you already know exp(z) is given by a power series from k is equal to 0 to infinity
19 00:01:44,014 –> 00:01:47,796 and then we have z to the power k divided by k factorial.
20 00:01:48,843 –> 00:01:54,383 Now I know the radius of convergence you have already calculated and we get r is infinity.
21 00:01:55,714 –> 00:01:59,560 This means that the exponential function is an entire function.
22 00:02:00,457 –> 00:02:06,201 So we know that the derivative of the exponential function exists everywhere and we can calculate it.
23 00:02:06,957 –> 00:02:10,556 We simply can do this in the series term by term.
24 00:02:11,543 –> 00:02:15,657 Hence here k comes in front and we reduce the power by 1.
25 00:02:16,157 –> 00:02:18,925 So you see, this is not complicated at all.
26 00:02:19,800 –> 00:02:28,046 However here please don’t forget, k=0 corresponds to the constant term, which always vanishes for the derivative.
27 00:02:29,129 –> 00:02:32,886 In other words the new series now should start with 1.
28 00:02:34,043 –> 00:02:39,659 Ok, now the nice thing we should see here is that we can cancel this k with k factorial.
29 00:02:40,771 –> 00:02:45,209 Therefore in the denominator only (k-1) factorial remains.
30 00:02:46,186 –> 00:02:52,740 So now this is a very nice expression and you see we can do an index shift to simplify it even more.
31 00:02:53,643 –> 00:03:03,085 So instead of starting with 1 we start with m=0 again and here please note, the new index m should represent k-1.
32 00:03:03,671 –> 00:03:08,170 Hence we have z to the power m divided by m factorial
33 00:03:09,186 –> 00:03:13,800 and with this result you see we get the original exponential function back.
34 00:03:14,714 –> 00:03:17,968 So taking the derivative does not change the function.
35 00:03:18,557 –> 00:03:23,715 In fact this means that all the derivatives of the exponential function are the same
36 00:03:24,700 –> 00:03:27,976 and this is an important property you should remember.
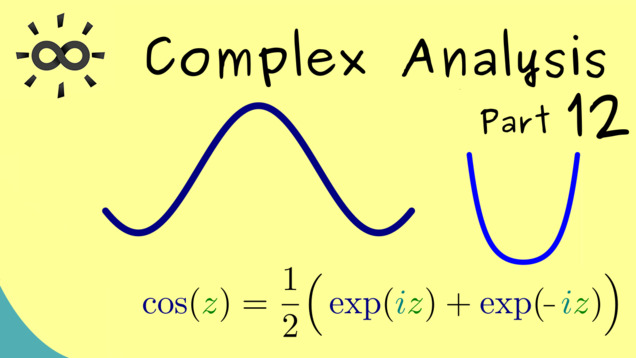
37 00:03:28,643 –> 00:03:37,913 Ok then let’s go to the next example. Which is the cos(z) and of course we also define this function via a power series.
38 00:03:38,543 –> 00:03:44,161 However this one is a little bit special, because only even powers of z occur here.
39 00:03:45,357 –> 00:03:49,757 For this reason we have to use the number 2 times k here and here.
40 00:03:50,386 –> 00:03:54,829 Otherwise you should recognize, it’s very similar to the exponential function.
41 00:03:55,629 –> 00:04:00,342 However there is also another difference, because there is a sign involved.
42 00:04:01,371 –> 00:04:05,143 So you see, some powers in this series get a minus sign.
43 00:04:06,143 –> 00:04:09,939 For example z to the power 2 gets a minus sign.
44 00:04:10,543 –> 00:04:15,990 Then z to the power 4 is plus again and z to the power 6 gets a minus sign again.
45 00:04:16,814 –> 00:04:21,344 Ok, there we have it. This is the definition of the complex cosine function
46 00:04:22,200 –> 00:04:27,753 and then I think you don’t have any problems calculating the derivative similarly to before.
47 00:04:28,429 –> 00:04:31,514 Therefore i would suggest that we do something else here
48 00:04:31,600 –> 00:04:36,286 and look which connection we find between the exponential function and the cosine function.
49 00:04:37,314 –> 00:04:43,959 Indeed we find something with the help of complex numbers, because “i” squared is -1.
50 00:04:44,557 –> 00:04:50,486 For this reason one idea would be to put “i” times z into the exponential function.
51 00:04:51,500 –> 00:04:55,324 This is not so complicated, because we have the whole power series here.
52 00:04:56,057 –> 00:05:01,968 Then what we should see is, here in the numerator we have essentially 4 different cases.
53 00:05:02,943 –> 00:05:07,070 We get this because the powers of “i” have a periodic structure.
54 00:05:07,671 –> 00:05:16,546 So maybe let’s start with the simplest case, when k=1. Then we simply have “i” times z to the power k.
55 00:05:17,500 –> 00:05:22,809 Of course this is not so surprising, but the same thing happens when k=5.
56 00:05:23,471 –> 00:05:33,153 We simply have this, because “i” to the power 5 is “i” again and of course this also holds when we increase k by 4.
57 00:05:34,343 –> 00:05:39,983 Okay, there you see we have one case where the factor in front of z to the power k is simply “i”.
58 00:05:41,000 –> 00:05:49,355 Now, in our next case this factor is -1. Of course this happens when we square our imaginary unit “i”.
59 00:05:50,057 –> 00:05:55,209 So it holds for k=2, k=6, k=10 and so on.
60 00:05:56,229 –> 00:06:01,379 Okay by having this you already see the next case should be k=3.
61 00:06:02,514 –> 00:06:11,013 Hence we need to know what “i” cubed is. You can say it’s “i” squared times “i”. Therefore simply “-i”.
62 00:06:12,000 –> 00:06:17,526 Now with this only the last case is missing, where we have k=0, 4 and so on.
63 00:06:18,329 –> 00:06:24,475 So let’s put this case at the top and then you should know, “i” to the power 4 is simply 1.
64 00:06:25,343 –> 00:06:30,057 Therefore in this case the factor in front of z to the power k is just 1.
65 00:06:30,771 –> 00:06:35,367 Ok, so you see this is very nice, but please keep our goal in mind.
66 00:06:35,743 –> 00:06:41,229 In order to get from the exponential function to the cosine, there shouldn’t be any “i” involved
67 00:06:41,714 –> 00:06:45,414 and also only the even case should matter here.
68 00:06:46,286 –> 00:06:54,660 Therefore we have to get rid of these two cases here and the idea is to do this with another exponential function.
69 00:06:55,486 –> 00:07:00,978 It turns out putting “-i” times z into the exponential function helps a lot.
70 00:07:01,429 –> 00:07:08,824 Of course the power series here looks very similarly to before and we also can consider 4 different cases.
71 00:07:09,643 –> 00:07:18,552 So maybe we can discuss them very quickly, because we only have to multiply with the factor -1 to the power k in these cases.
72 00:07:19,557 –> 00:07:26,315 Hence for the even numbers we don’t change anything and for the odd numbers a -1 is included.
73 00:07:27,000 –> 00:07:31,983 So let’s copy the cases there and there and add a minus sign for the odd cases.
74 00:07:32,471 –> 00:07:35,444 Hence minus here and plus there.
75 00:07:36,443 –> 00:07:44,696 Ok, so you see here our idea is now, that we look at the sum exp(iz) plus exp(-iz).
76 00:07:45,300 –> 00:07:53,461 Then you see the terms where “i” is involved will simply cancel out and only the terms with an even k remain.
77 00:07:54,357 –> 00:07:58,232 Then you see, this is almost what we want for the cosine.
78 00:07:59,000 –> 00:08:03,511 Ok, maybe to make the whole thing here clearer, let’s use the index m again.
79 00:08:04,286 –> 00:08:13,255 Now please recall, only the even powers are involved. So our exponent is 2 times m and in the denominator we have 2m factorial.
80 00:08:14,229 –> 00:08:19,934 However please be careful. We also have a sign involved, depending in which case we are.
81 00:08:20,443 –> 00:08:24,381 Hence we have to add the factor -1 to the power m
82 00:08:24,857 –> 00:08:29,243 Moreover also please don’t forget, we have the addition here.
83 00:08:29,300 –> 00:08:34,957 So we add the two cases or to put it in other words, we also get a factor 2.
84 00:08:35,900 –> 00:08:43,108 Ok, now we are finished and you see with the exception of this factor, this is exactly our cos(z).
85 00:08:43,943 –> 00:08:49,768 Of course that was our goal. Now we have the relation between cosine and the exponential function.
86 00:08:50,729 –> 00:08:56,151 This is very nice, because we can also use this relation to calculate the derivative.
87 00:08:56,700 –> 00:09:05,237 So first let’s state the formula again. Cosine can be written as 0.5 times (exp(iz) plus exp(-iz)).
88 00:09:06,143 –> 00:09:11,761 Then of course we can simply use the chain rule to calculate the derivative of cos(z).
89 00:09:12,771 –> 00:09:16,629 Now the inner derivative gives us the factor “i” in front.
90 00:09:17,029 –> 00:09:22,414 This happens for the first and the second exponential, but the second also gets a minus sign
91 00:09:23,086 –> 00:09:28,855 and otherwise we can simply use the fact, that the derivative of the exponential is the exponential again.
92 00:09:29,557 –> 00:09:37,495 There we have it this is the derivative of the cosine and you might already know, this should be -sin(z).
93 00:09:38,457 –> 00:09:43,847 Hence also for the sine we now have a representation with exponential functions
94 00:09:44,600 –> 00:09:51,425 and now these two representations can be very helpful, when you do calculations with cosine and sine involved.
95 00:09:52,300 –> 00:09:58,594 Simply because powers of exponential functions are easier to deal with than powers of cosine or sine.
96 00:09:59,471 –> 00:10:07,342 However in our course here, it’s very important to know that exp, cos and sin are all holomorphic functions.
97 00:10:08,243 –> 00:10:15,929 Ok, I think that’s good enough for today and I really hope that I see you in the next video. Have a nice day and bye!
-
Quiz Content
Q1: Let the power series $f: \mathbb{C} \rightarrow \mathbb{C}$ be given by $f(z) = \sum_{k=0}^\infty a_k z^k$. What is the derivative?
A1: $f^\prime(z) = \sum_{k=0}^\infty a_k z^k$
A2: $f^\prime(z) = \sum_{k=0}^\infty k a_k z^k$
A3: $f^\prime(z) = \sum_{k=1}^\infty k a_k z^{k-1}$
Q2: We define the sine function by $$\sin(z) = \sum_{k=0}^\infty \frac{ (-1)^k }{ (2k+1)! } z^{2k+1}$$ What is the derivative?
A1: $\cos(z)$
A2: $-\cos(z)$
A3: $i \cos(z)$
A4: $2 \cos(z)$
Q3: What is an alternative description of the sine function?
A1: $\sin(z) = $ $ \exp(z) + \exp(iz)$
A2: $\sin(z) = $ $ \frac{1}{2} (\exp(z) + \exp(iz))$
A3: $\sin(z) = $ $ \frac{1}{2i} (\exp(iz) - \exp(-iz))$
A4: $\sin(z) = $ $ \frac{1}{2} (\exp(iz) + \exp(-iz))$
-
Last update: 2025-09