-
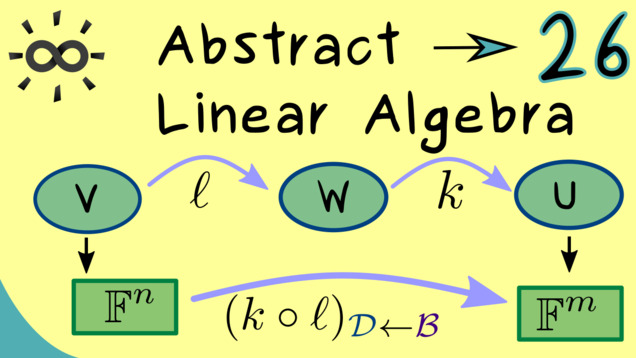
Title: Matrix Representations for Compositions
-
Series: Abstract Linear Algebra
-
YouTube-Title: Abstract Linear Algebra 26 | Matrix Representations for Compositions
-
Bright video: https://youtu.be/YD92kR-Xqz8
-
Dark video: https://youtu.be/QGfwW008hM4
-
Quiz: Test your knowledge
-
Dark-PDF: Download PDF version of the dark video
-
Print-PDF: Download printable PDF version
-
Thumbnail (bright): Download PNG
-
Thumbnail (dark): Download PNG
-
Subtitle on GitHub: ala26_sub_eng.srt missing
-
Timestamps (n/a)
-
Subtitle in English (n/a)
-
Quiz Content
Q1: Let $V, W$ be two finite-dimensional $\mathbb{F}$-vector spaces, and $\ell: V \rightarrow W$, $k: W \rightarrow V$ linear maps. What is always correct about a matrix representation of $k \circ \ell$?
A1: It’s a square matrix.
A2: It’s an invertible matrix.
A3: It’s an orthogonal matrix.
A4: It’s a unitary matrix.
Q2: Let $V,W$ be two $\mathbb{F}$-vector spaces of dimension $2$, and $\ell: V \rightarrow W$, $k: W \rightarrow V$ linear maps, with matrix representations $\begin{pmatrix} 2 & 1 \ 3 & 1 \end{pmatrix}$ and $\begin{pmatrix} 1 & 0 \ 0 & 1 \end{pmatrix}$, respectively. What is always correct about a matrix representation of $k \circ \ell$?
A1: It’s given by $\begin{pmatrix} 2 & 1 \ 3 & 1 \end{pmatrix}$.
A2: It’s given by $\begin{pmatrix} 1 & 0 \ 0 & 1 \end{pmatrix}$.
A3: It’s given by $\begin{pmatrix} 1 & 1 \ 1 & 1 \end{pmatrix}$.
A4: It’s an invertible matrix.
Q3: Let $V$ be an $\mathbb{F}$-vector spaces of dimension $2$ and $\ell: V \rightarrow V$ be a linear map with matrix representation $\begin{pmatrix} 2 & 5 \ 1 & 2 \end{pmatrix}$. What is a matrix representation of $ \ell^{-1} $?
A1: $\begin{pmatrix} 2 & 1 \ 2 & 1 \end{pmatrix}$.
A2: $\begin{pmatrix} 1 & 0 \ 0 & 0 \end{pmatrix}$.
A3: $\begin{pmatrix} 1 & 1 \ 1 & 1 \end{pmatrix}$.
A4: Every $2\times2$-matrix can be a valid matrix representation of $ \ell^{-1} $.
A5: $\begin{pmatrix} -2 & 5 \ 1 & -2 \end{pmatrix}$.
-
Last update: 2024-11