Information about Functional Analysis - Part 34

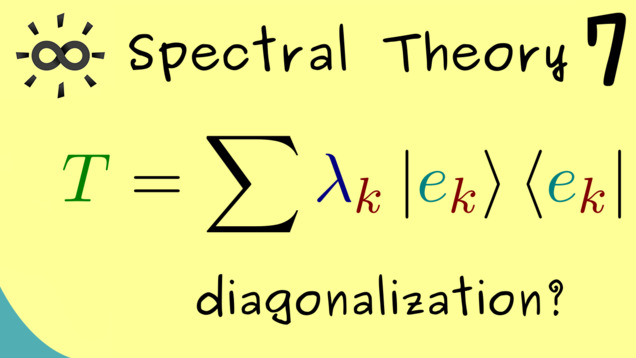
Title: Spectral Theorem for Compact Operators

Series: Functional Analysis

YouTube-Title: Functional Analysis 34 | Spectral Theorem for Compact Operators

Bright video: https://youtu.be/0a8zNP8kmSE

Dark video: https://youtu.be/roU6pTjf5h8

Quiz: Test your knowledge

PDF: Download PDF version of the bright video

Print-PDF: Download printable PDF version

Thumbnail (bright): Download PNG

Back to overview page