Here, you find my whole video series about Start Learning Numbers in the correct order and I also help you with some text around the videos. If you have any questions, you can use the comments below and ask anything. However, without further ado let’s start:
Part 1 - Natural Numbers (in Set Theory)
Start Learning Numbers is a video series I started for everyone who is interested in the necessary foundations you need to enjoy the whole world of mathematics. Now by knowing the basics in set theory, we are able to construct of known mathematics just out of sets. This makes everything stands on solid grounds. We start with the natural numbers.

Part 2 - Natural Numbers (Successor Map and Addition)
The natural numbers have a recursive property one can use for definitions:
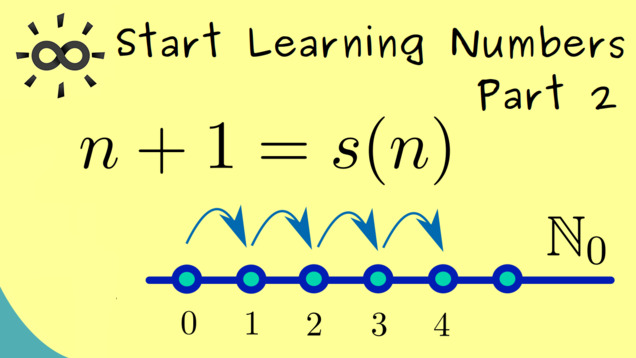
Part 3 - Natural Numbers (Induction and Associativity
The whole concept leads the mathematical induction, which helps a lot in proofs:

Part 4 - Natural Numbers (Ordering)
Let us talk about the ordering the natural numbers have:

Part 5 - Natural Numbers (Multiplication)
The next operation for the natural numbers is the multiplication:

Part 6 - Integers (Construction)
Having all these things, we can start talking about the integers. Let us construct them using pairs of natural numbers:

Part 7 - Integers (Addition and Inverses)
What are the important properties of the integers?

Part 8 - Integers (Multiplication)
The integers also need a multiplication which we can define using the already known multiplication of natural numbers:

Part 9 - Rational Numbers (Construction)
Next on our list of number sets we want to construct are the fractions, the rational numbers:

Part 10 - Rational Numbers (Addition and Multiplication)
The rational numbers form a so-called field:

Part 11 - Rational Numbers (Ordering)
The only thing that we have to add to rational numbers now is an ordering, which conserves the ordering from the other number sets:

Go to the next course
Start Learning Logic
Start Learning Sets
Start Learning Numbers
Start Learning Reals
Start Learning Complex
Summary of the course Start Learning Numbers
- You can download the whole PDF here and the whole dark PDF.
- You can download the whole printable PDF here.