Here, you find my whole video series about Manifolds, which you could see as generalised surfaces, in the correct order. I also help you with some text and explanations around the videos. If you want to test your knowledge, please use the corresponding quiz after watching the video. Moreover, you can also consult the PDF version of the video if needed. In the case you have any questions about the topic, you can contact me or use the community discussion in Mattermost and ask anything. However, without further ado let’s start:
Part 1 - Introduction and Topology
Manifolds is a video series I started for everyone who is interested in calculus on generalised surfaces one usually calls manifolds when some rules are satisfied. Some basic facts from my Real Analysis course and from my Functional Analysis course are helpful but I try to be as self-contained as possible. Let us start with the introduction and the definition of a topology.
Content of the video:
00:00 Introduction
00:20 Overview
02:24 Stoke’s theorem as the goal
02:56 Metric Spaces
04:56 Definition Topology
07:29 Simple examples of topological spaces
09:07 Credits
With this you now know the foundations that we will need to start with this series. We will always work with topologies. So let us define some more notions.
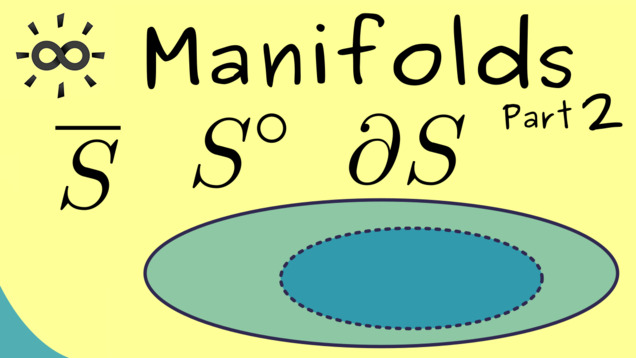
Part 2 - Interior, Exterior, Boundary, Closure
The notion of a interior point is something that comes immediately out when you look at the definition of a topology, which fixes open sets. More notions like closure and boundary of a set will also be explained now:
Part 3 - Hausdorff Spaces
Like in metric spaces, convergence is very important topic for a lot of calculations, like limits, derivatives and so on. It turn out that we need so-called Hausdorff spaces to get similar results:
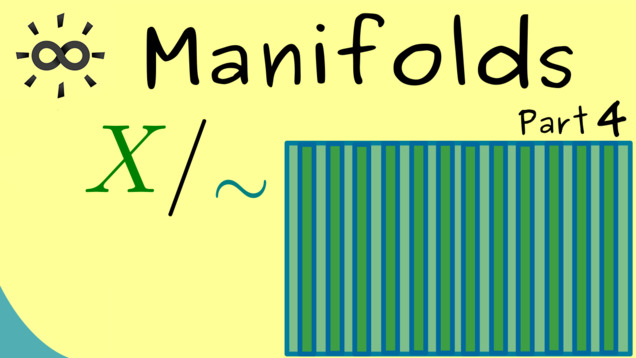
Part 4 - Quotient Spaces
One important tool to construct new topological spaces is given by equivalence relations. This leads to a so-called quotient topology:
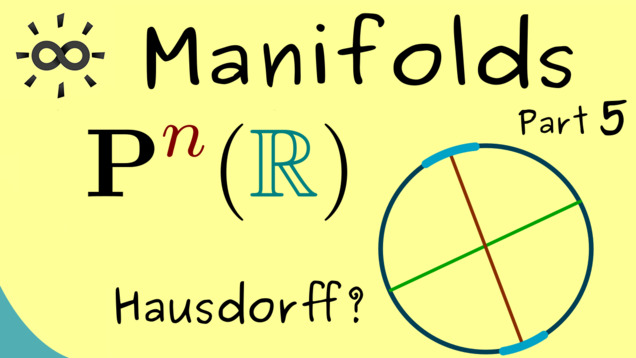
Part 5 - Projective Space
Let us talk more about projective space which is defined by a quotient space:
Part 6 - Second-Countable Space
Now we introduce the concept of second-countable spaces which we need later to define manifolds. For this reason, we first need to define the notion of a base or basis of a topology.
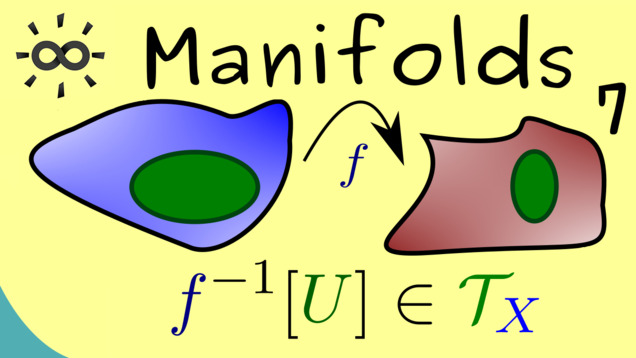
Part 7 - Continuity
The next notion describes one of the most important concepts in topology: continuous maps. They are important because the conserve the whole structure of a topological space. Therefore, for invertible maps, we introduce the natural definition of a homeomorphism.
Part 8 - Compactness
A concept we will also need in the series about manifolds is known as compact sets:
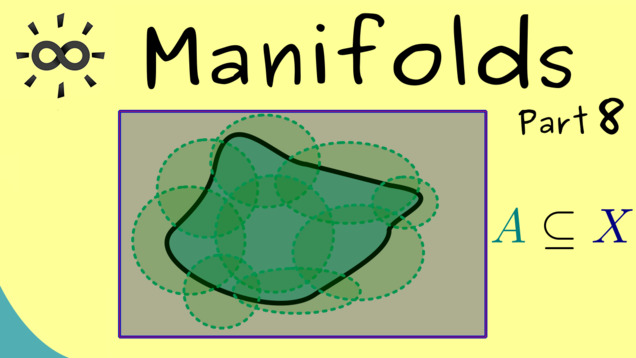
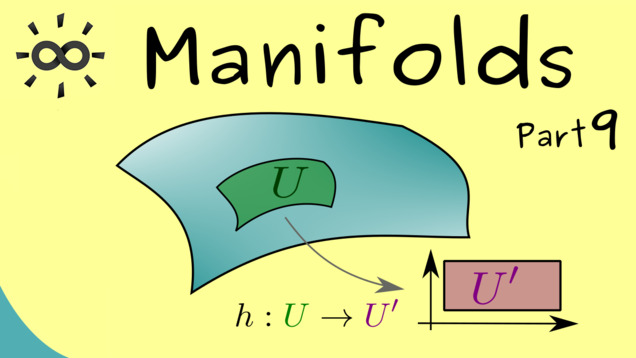
Part 9 - Locally Euclidean Spaces
Finally, we can talk about the definition of a manifold. We combine three properties and the last property will be called locally Euclidean, which means that a manifold can be flattened at least locally. We will use charts to do that. A whole collection of charts that cover the whole manifold is called an atlas.
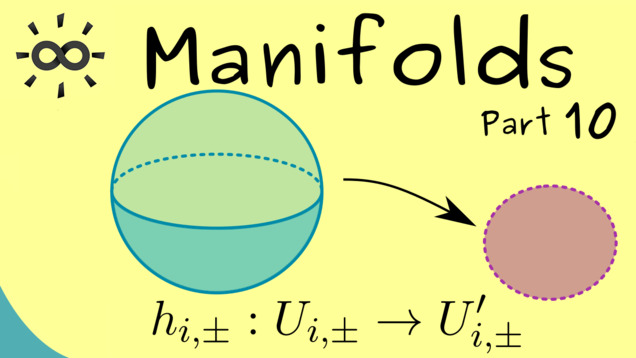
Part 10 - Examples for Manifolds
Let’s look at examples for manifolds.
Part 11 - Projective Space is a Manifold
Another example for an abstract manifold is given by the projective space.
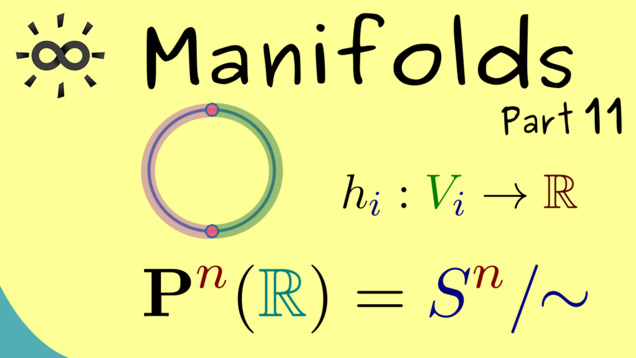
Part 12 - Smooth Structures
Now we are ready to include more structure on our topological manifolds. These will be so-called smooth structures and they will make the manifold to a smooth manifold. Indeed, these will be the objects we want to study because there we can do calculus.
Part 13 - Examples of Smooth Manifolds
Let us look at examples for such smooth structures and smooth manifolds. A lot of manifolds we discussed before already carry a smooth structure.
Part 14 - Submanifolds
Next, we discuss the notion of submanifolds, which is just a manifold found inside a larger one. Especially submanifolds of $ \mathbb{R}^n $ will be important later.
Part 15 - Regular Value Theorem in $\mathbb{R}^n$
For manifolds in $\mathbb{R}^n$, we have a nice theorem. It’s possible to describe them as preimages of regular values. This is known as the regular value theorem.
Part 16 - Smooth Maps (Definition)
By lifting the notion of differentiability from $ \mathbb{R}^n $ to manifolds with the help of charts, we can define so-called smooth maps between two smooth manifolds.
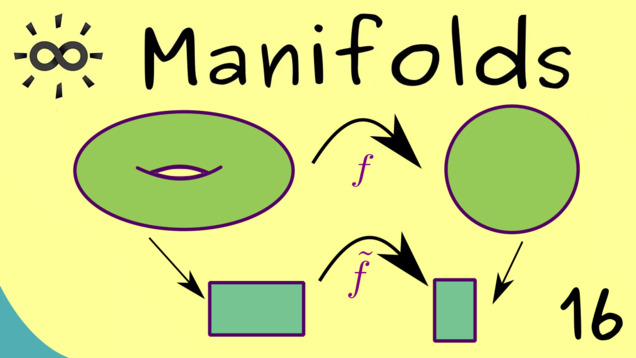
Part 17 - Examples of Smooth Maps
After defining the concept of a smooth map, we can look at some examples.
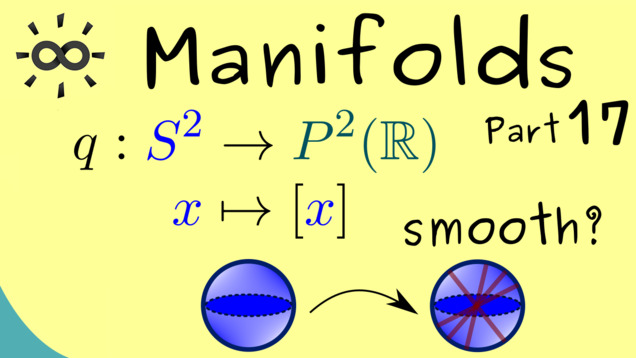
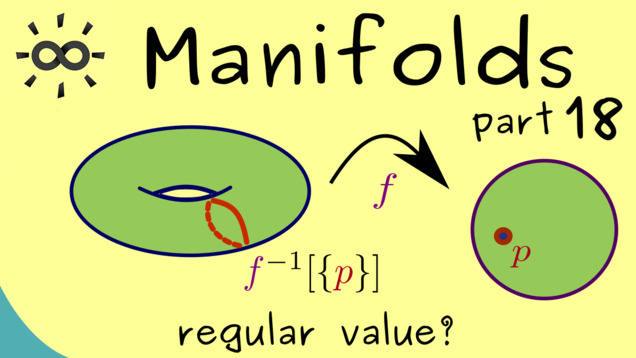
Part 18 - Regular Value Theorem (abstract version)
We already discussed the regular value theorem for submanifolds in $ \mathbb{R}^n $. However, we can lift the whole theorem to the abstract level and see that it also holds for submanifolds in any manifold.
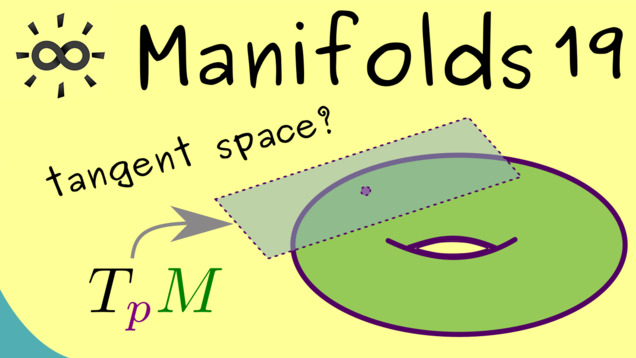
Part 19 - Tangent Space for Submanifolds
This is the point where we introduce the first version for a tangent space. It’s very demonstrative to define this notion for submanifolds first.
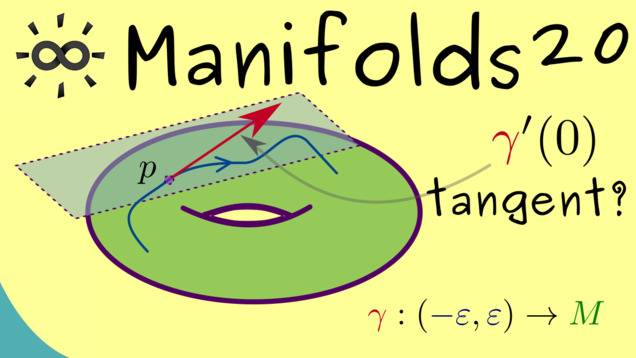
Part 20 - Tangent Curves
In the next video, we want to give an alternative definition for the tangent space. This one has the advantage that we can also generalise it for abstract manifolds, which are not given as subsets of $ \mathbb{R}^n $. This will be the notion we will use for the rest of the series. It will be needed to define the differential of a smooth map.
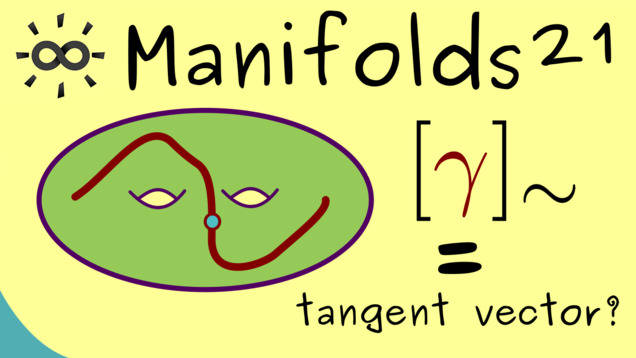
Part 21 - Tangent Space (Definition via tangent curves)
Now we can finally define the tangent space in the general context, which means for every smooth manifold. For this, we will take the knowledge from the tangent curves from the last video and try to describe the essence of tanget vectors such that they also make sense for abstract manifolds that are not submanifolds in $ \mathbb{R}^n $. This will be done with equivalent relations and equivalence classes.
Part 22 - Coordinate Basis
For understanding the definition of the tangent space, it is helpful to describe it with basis vectors. Since we have an isomorphism with local charts, we can check what happens for the canonical basis from $ \mathbb{R}^n $ under this map. What we get is a basis in $ T_p(M) $, which we denote by $ ( \partial_1, \ldots, \partial_n ) $.
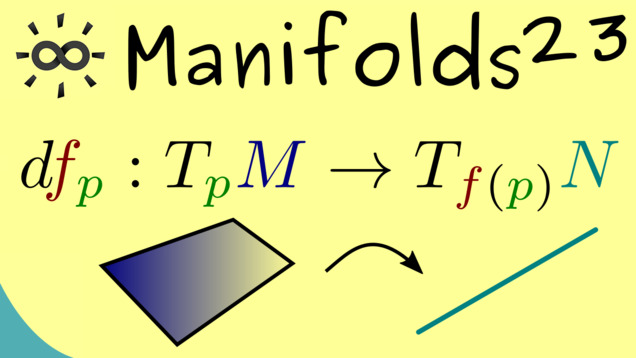
Part 23 - Differential (Definition)
After all this work and discussions about tangent spaces, we are now ready to define the differential of a smooth map, denoted by $d f_p$. We also define a new manifold as the disjoint union of all tangent spaces and call it the tangent bundle, denoted by $ TM $.
Part 24 - Differential in Local Charts
Here we look at the relation of the differential and the common Jacobian.
Part 25 - Differential (Example)
In this video, we discuss the notion of directional derivative again and will look at some concrete example for a differential of a smooth map.
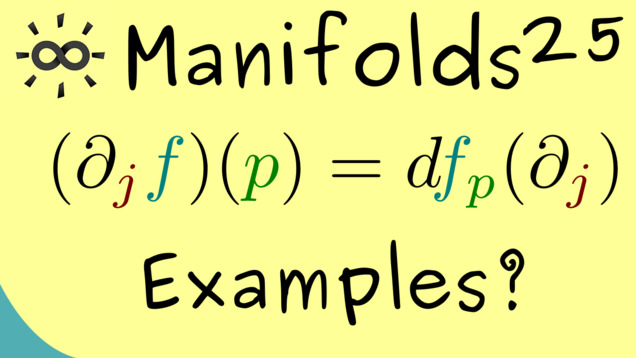
Part 26 - Ricci Calculus
Let’s talk a little bit about the Ricci calculus, also called tenso calculus. We just give a short introduction how to translate the objects we discuss before into this new language. One important ingredient is that one suppresses a lot of details and deals with superscripts and subscripts for variables. This leads us to contravariant and covariant vectors, where more details will be discussed in future videos.
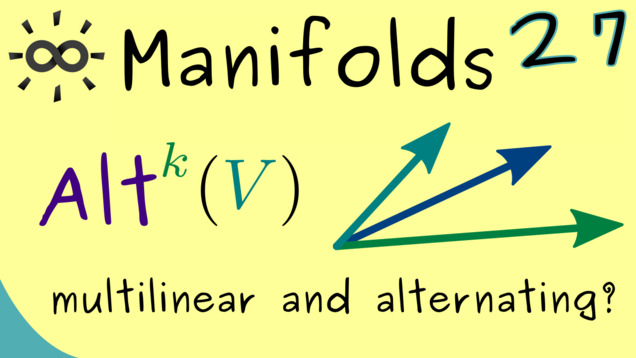
Part 27 - Alternating k-forms
For defining integration on manifolds, we have to some groundwork first. This means we have to learn some multilinear algebra, in particular, so-called alternating multilinear maps. In short, we will just call them k-forms.
Part 28 - Wedge Product
After introducing k-forms, we can also define a multiplication for the space of alternating multilinear maps. This is related to the tensor-product but this special version is called wedge-product because it’s written as $ \alpha \wedge \beta $.
Part 29 - Differential Forms
Finally, we can give the explicit definition of a differential form on a manifold. We will use them later for integration on manifolds.
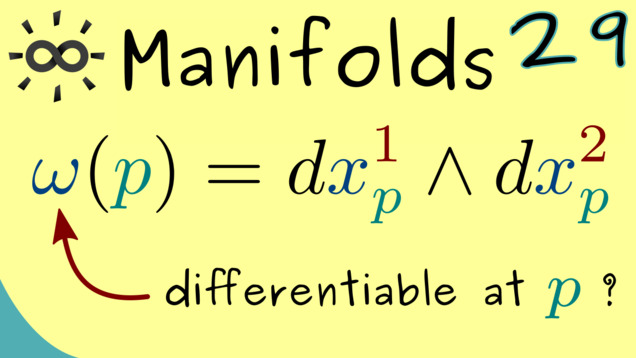
Part 30 - Examples of Differential Forms
In order to understand how differential forms, we should look at some simple and important examples. We don’t have to go into complicated manifolds because the euclidean space already offers some important differential forms. In particular, we will look at volume forms and polar coordinates.
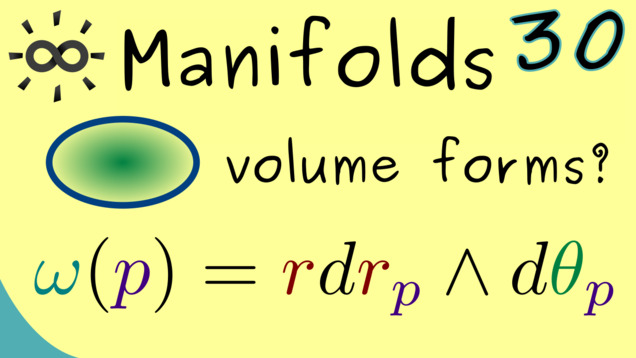
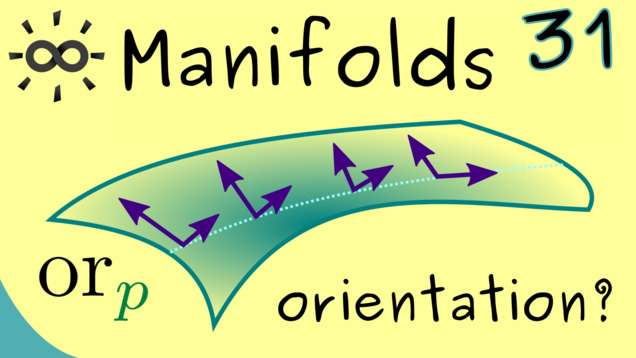
Part 31 - Orientable Manifolds
Here, let’s talk about orientated vector spaces. This means we distinguish positively orientated bases and negatively orientated bases. By applying this to manifolds, we can define so-called orientable manifolds, which will be very important for integration theorems later. However, it turns out that not all manifolds are orientable. The best-known counterexample is the Möbius strip.
Part 32 - Alternative Definitions for Orientations
It turns out that one has more possibilities for defining orientations on manifolds. Here we will prove one equivalence and state another.
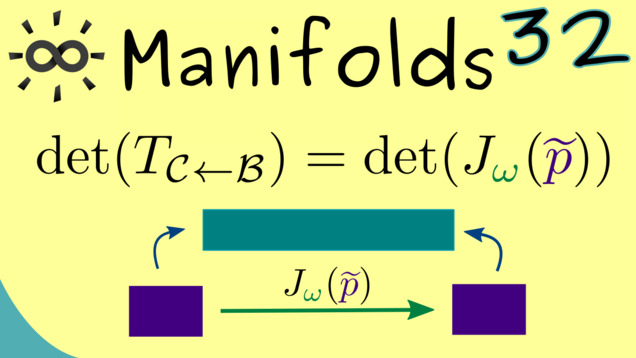
Part 33 - Riemannian Metrics
With this video we finally put some geometry to the manifolds. These is done by using the tangent spaces at each point an inner products in them. The collection of all these inner products is usually called a Riemannian metric, named after the German mathematician Bernhard Riemann. Moreover, a smooth manifold together with a Riemannian metric is called a Riemannian manifold. These manifolds allow for a lot of calculations, like distances, angles, areas, and so on. Therefore, there are many applications for these manifolds, which we will discuss later on.
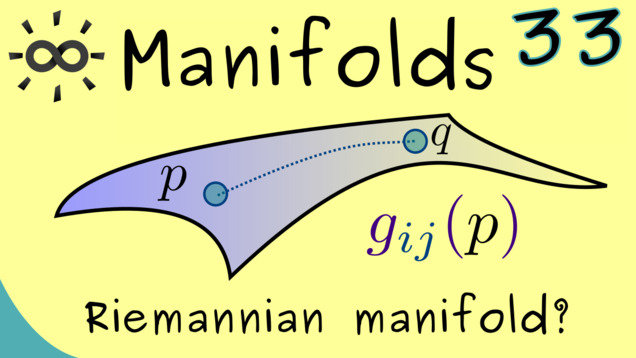
Part 34 - Examples for Riemannian Manifolds
Let’s look at some examples to get an idea how Riemannian metrics work. Indeed, for submanifolds in $ \mathbb{R}^n $, we should have a standard Riemannian metric coming from the standard inner product. We should check if everything fits together with our intuition and knowledge for geometry.
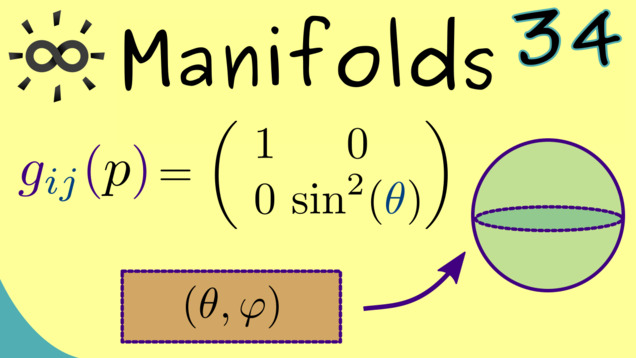
Part 35 - Canonical Volume Forms
We already know that the orientable manifolds have non-trivial volum forms. More precisely, if the dimension of $ M $ is $ n $, the there is a non-zero $ \omega \in \Omega^n(M) $. It turn out that for Riemannian manifolds we can choose a so-called canonical volume form, which is normalized with respect to the Riemannian metric.
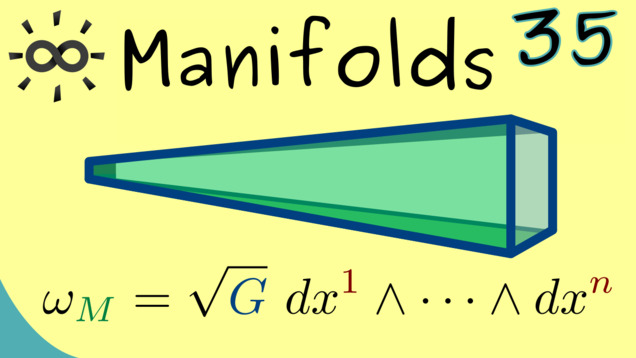
Part 36 - Examples for Canonical Volume Forms
After the precise definition of canonical volume forms, we are ready to consider some concrete examples. In fact, we already know it for the sphere $S^2$. Let’s also look at graph surfaces in $ \mathbb{R}^3 $, which can be described by functions $ f: \mathbb{R}^2 \rightarrow \mathbb{R} $.
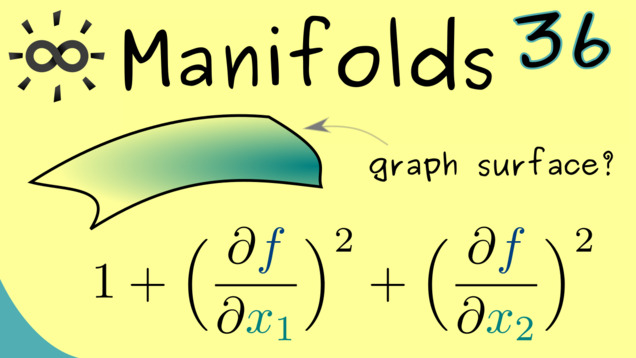
Part 37 - Unit Normal Vector Field
Before dive into integration on manifolds, I want to point out that canonical volume forms for submanifolds can be very easy to understand if you have a so-called continuous unit normal vector field.
Part 38 - Integration for Differential Forms
Now finally, let’s start the integration theory for manifolds. We require some knowledge about Riemann integrals or Lebesgue integrals, which you can find in the Real Analysis courseand the Measure Theory course, respectively. So let’s first get a visualization about that. The best way to do this is to see the function inside the integral as a density. This gives us the correct connection to the integral of a differential form.
Part 39 - Integration on a Chart (Definition)
Now that we know that differential forms are the correct objects in an integration, we can try to lift the results from $ \mathbb{R}^n $ to general manifolds. This can just be done with a parameterization $ \varphi : \widetilde{U} \rightarrow U $. Therefore, we start our definition for integration by considering a single chart $ (U,h) $ first. On this one, we could motivate a decomposition like one does it for the Riemann integral and we get an nice general formula out.
Part 40 - Integral Is Well-Defined
This video is a little bit technical because we have to show the integral $ \int \omega $ is well-defned, which means that is does not depend on the chosen chart. One can say that this is some sort of substitution rule for this abstract integral. Indeed, it turns out that the common change-of-variable formula is the key ingredient in this prooof.
Part 41 - Measurable Sets and Null Sets
At the moment, we can only calculate integrals that completely lie inside a single chart. However, for a lot of applications, this is already sufficient if we are able to exclude some sets that have a volume of zero. In the common matter of speaking, we call these sets null sets. So let’s look at an example and at the general definition.
Part 42 - Integrable Differential Forms
Let’s continue the discussion about the definition of the integration. Here we will finally define the integral over a whole manifold. For this we have to consider countably many charts to split the manifold up. This is always possible because a manifold is second-countable by definition which implies that there is a countable atlas $ (U_k, h_k)_{k \in \mathbb{N} } $.
Part 43 - Integral is Well-Defined
The definition of the last video had one little flaw: we don’t know if two different decompositions lead to the same integral in the end. The proof of this fact will be the content of this video. It’s not hard to show if you already know how to deal with integrals in $ \mathbb{R}^n $.
Part 44 - Change of Variables
We already talked about the change of variables formula for integrals in $\mathbb{R}^n$. Since the integration on manifolds is defined by the common integration in $\mathbb{R}^n$, we can also lift this change of variables formula. What we get is an ** abstract change of variables formula** for manifolds. It’s really easy to remember and we can also prove it.
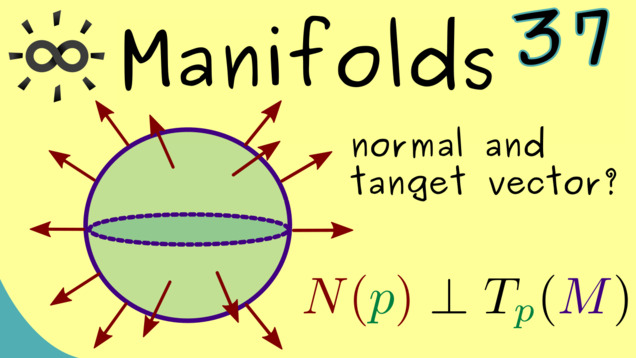
Summary of the course Manifolds
- You can download the whole PDF here and the whole dark PDF.
- You can download the whole printable PDF here.
- Test your knowledge in a full quiz.